sin

sin

A function that can be used in Formulas.

Syntax and semantics

sin (x): compute the sine of x.

   Axes: -5, 5, -1.1, 1.1

   Draw inner box

   Draw function: -5, 5, 1000, ~ sin (x)

   One mark bottom: -3*pi/2, "no", "yes", "yes", "\-m3%\pi/2"

   One mark bottom: -pi, "no", "yes", "yes", "\-m%\pi"

   One mark bottom: -pi/2, "no", "yes", "yes", "\-m%\pi/2"

   One mark bottom: 0, "no", "yes", "yes", "0"

   One mark bottom: pi/2, "no", "yes", "yes", "+%\pi/2"

   One mark bottom: pi, "no", "yes", "yes", "+%\pi"

   One mark bottom: 3*pi/2, "no", "yes", "yes", "+3%\pi/2"

   One mark left: -1, "no", "yes", "yes", "\-m1"

   One mark left: 0, "no", "yes", "yes", "0"

   One mark left: 1, "no", "yes", "yes", "+1"

   Text bottom: "yes", "%x \->"

   Text left: "yes", "##sin# (%x)"

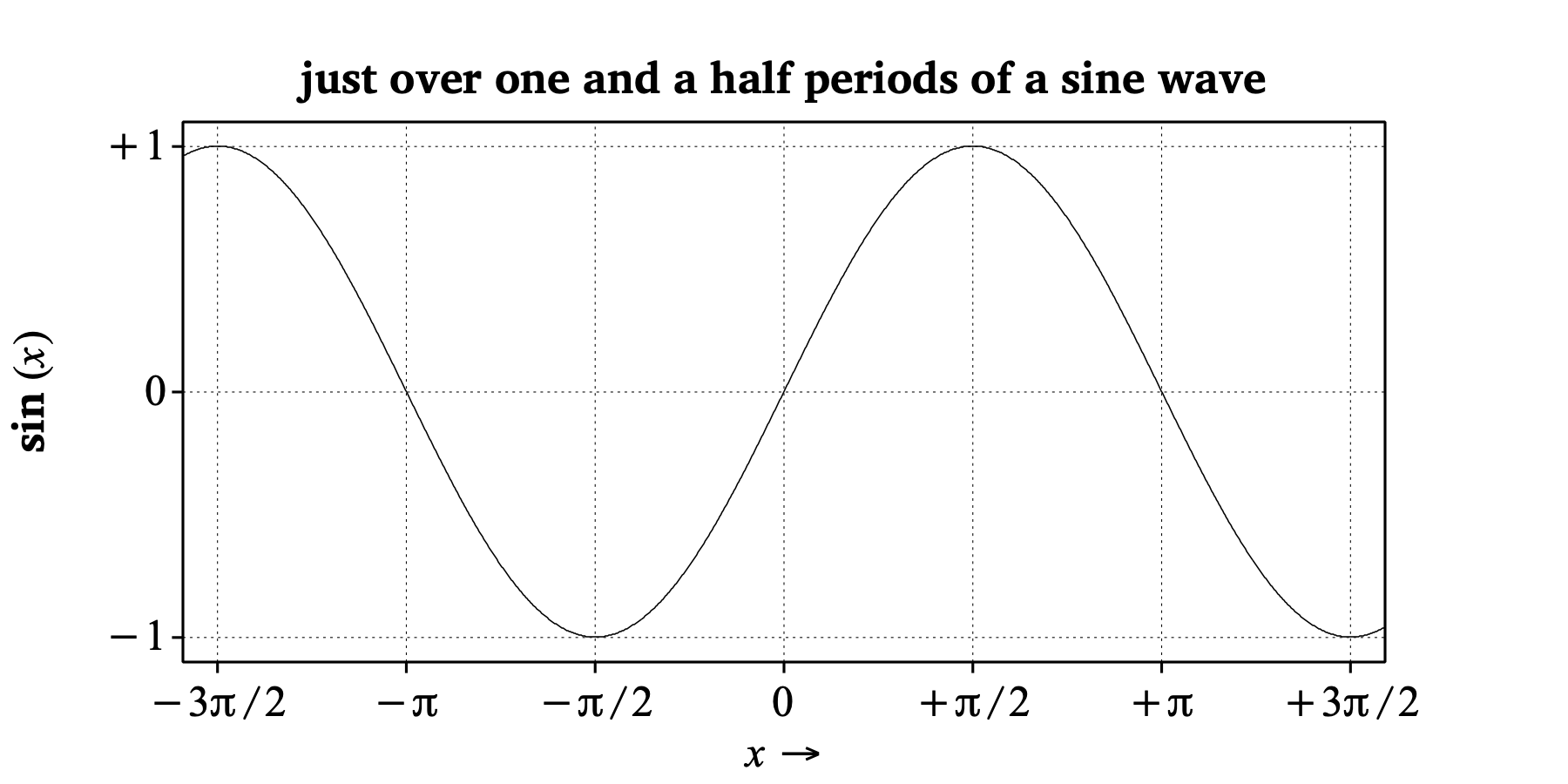
   Text top: "no", "##just over one and a half periods of a sine wave"

This picture illustrates the following properties of the sine function:

• sin (x) is zero for all values of x that are integer multiples of π.

• The extrema of sin (x) are −1 and +1.

• sin (x) is −1 or +1 wherever x is an odd multiple of π/2.

• The function is periodic with period 2π, i.e., sin (x+2π) = sin (x).

• The function is symmetric around π/2, i.e. sin (π/2−x) = sin (x).

• The function is antisymmetric around 0, i.e. sin (−x) = − sin (x); in other words, if you take the sine curve and rotate it by 180 degrees around the origin (i.e. the point (0, 0)), then you get the same curve again.

Syntax and semantics

Links to this page