cos

cos

A function that can be used in Formulas.

Syntax and semantics

cos (x): compute the cosine of x.

   Axes: -5, 5, -1.1, 1.1

   Draw inner box

   Draw function: -5, 5, 1000, ~ cos (x)

   One mark bottom: -3*pi/2, "no", "yes", "yes", "\-m3%\pi/2"

   One mark bottom: -pi, "no", "yes", "yes", "\-m%\pi"

   One mark bottom: -pi/2, "no", "yes", "yes", "\-m%\pi/2"

   One mark bottom: 0, "no", "yes", "yes", "0"

   One mark bottom: pi/2, "no", "yes", "yes", "+%\pi/2"

   One mark bottom: pi, "no", "yes", "yes", "+%\pi"

   One mark bottom: 3*pi/2, "no", "yes", "yes", "+3%\pi/2"

   One mark left: -1, "no", "yes", "yes", "\-m1"

   One mark left: 0, "no", "yes", "yes", "0"

   One mark left: 1, "no", "yes", "yes", "+1"

   Text bottom: "yes", "%x \->"

   Text left: "yes", "##cos# (%x)"

   Text top: "no", "##just over one and a half periods of a (co)sine wave"

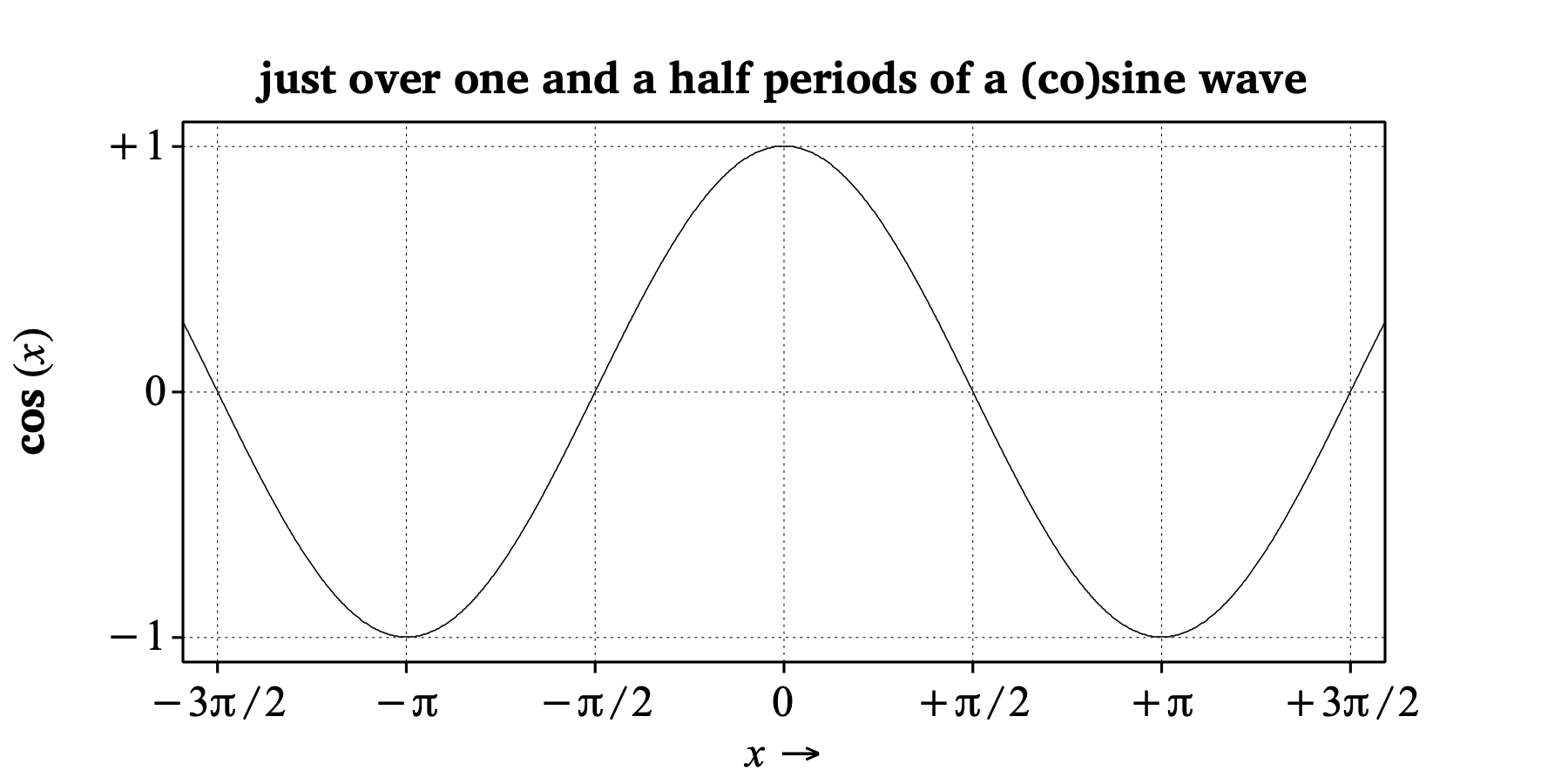
This picture illustrates the following properties of the cosine function:

• cos (x) is zero for all values of x that are odd multiples of π/2.

• The extrema of cos (x) are −1 and +1.

• cos (x) is −1 or +1 wherever x is an integer multiple of π.

• The cosine function is periodic with period 2π, i.e., cos (x+2π) = cos (x).

• The cosine function is symmetric around 0, i.e. cos (−x) = cos (x).

• The cosine function is antisymmetric around π/2, i.e. cos (π/2−x) = − cos (x); in other words, if you take the cosine curve and rotate it by 180 degrees around the point (π/2, 0), then you get the same curve again.

A cosine wave is a special case of the more general sine wave that is given by y = sin (x + φ), where φ (an additive constant called the initial phase) is π/2.

Syntax and semantics

Links to this page