A command to create a PointProcess object that represents a Poisson process. A Poisson process is a stationary point process with a fixed density λ, which means that there are, on the average, λ events per second.

Settings

Start time (s)

t_min, the beginning of the time domain, in seconds.

End time (s)

t_max, the end of the time domain, in seconds.

Density (Hz)

the average number of points per second (λ).

Algorithm

First, the number of points N in the time domain is determined. Its expectation value is

but its actual value is taken from the Poisson distribution:

Then, N points are computed throughout the time domain, according to a uniform distribution:

Example

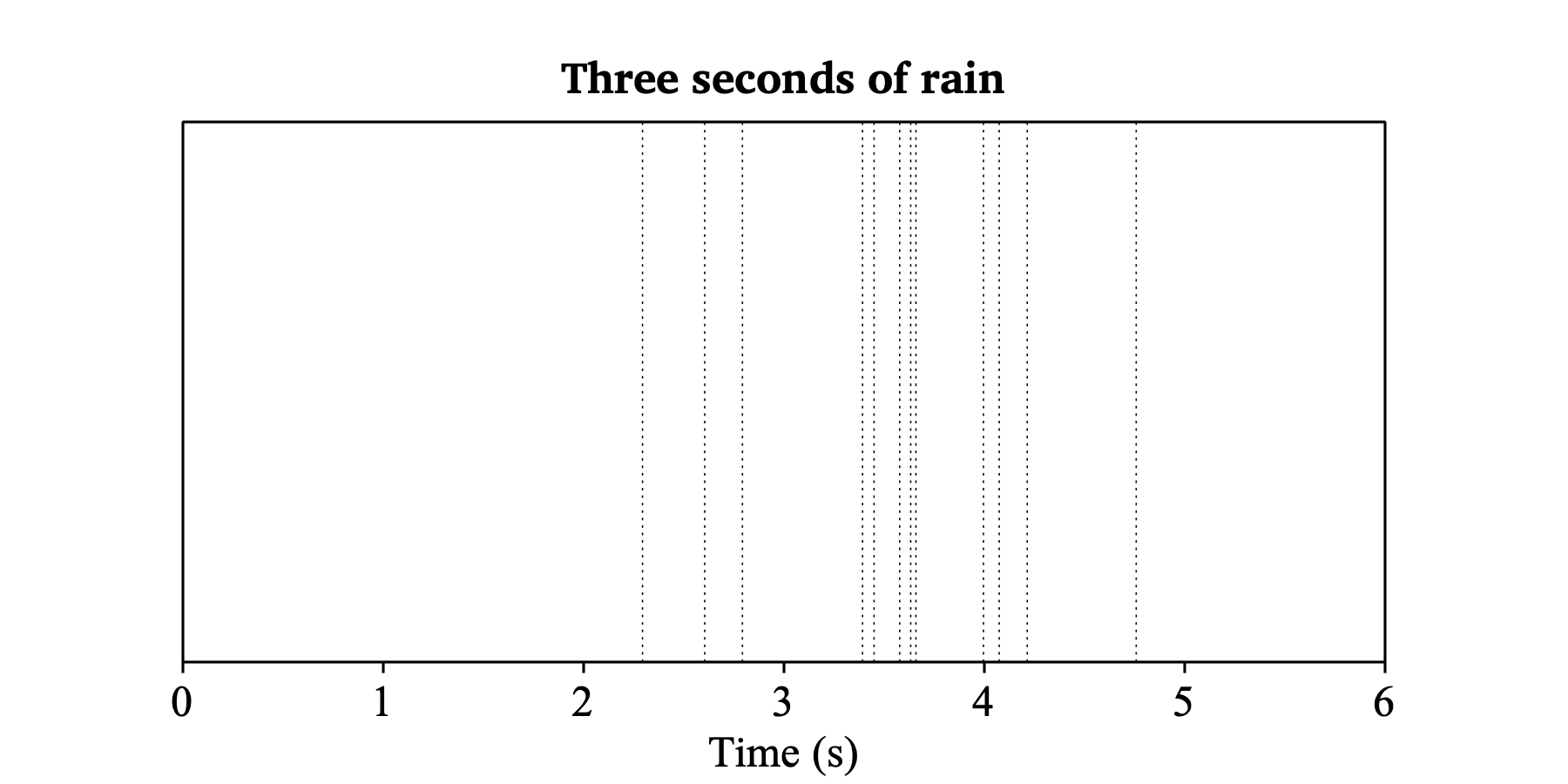
Suppose that it rains between t_min = 2.0 seconds and t_max = 5.0 seconds, with an average of 4.0 drops per second expected to fall on my head. To simulate this process, you can click (or script) the following commands:

When you refresh this picture, e.g. by clicking on the “> 1” button and then on the “1 <” button, you will see that the points lie at different time points each time. This variation is due to the stochasticity of the Poisson process: the points occur at random places.

Also, the number of points varies: on average, there will be 12 points, but there can just as easily be 10 or 15 points. As the rain shower lasts 3.0 seconds, the expected total number of drops on my head is λ = 3.0 seconds · 4.0 drops/second = 12.0 drops, but the actual number of points is just as stochastic as their locations in time are.

Fast implementation

One can simulate the number of points and their times as follows. To show that our fast implementation does exactly the same as Create Poisson process... does, we first make sure that the points lie at reproducible time points:

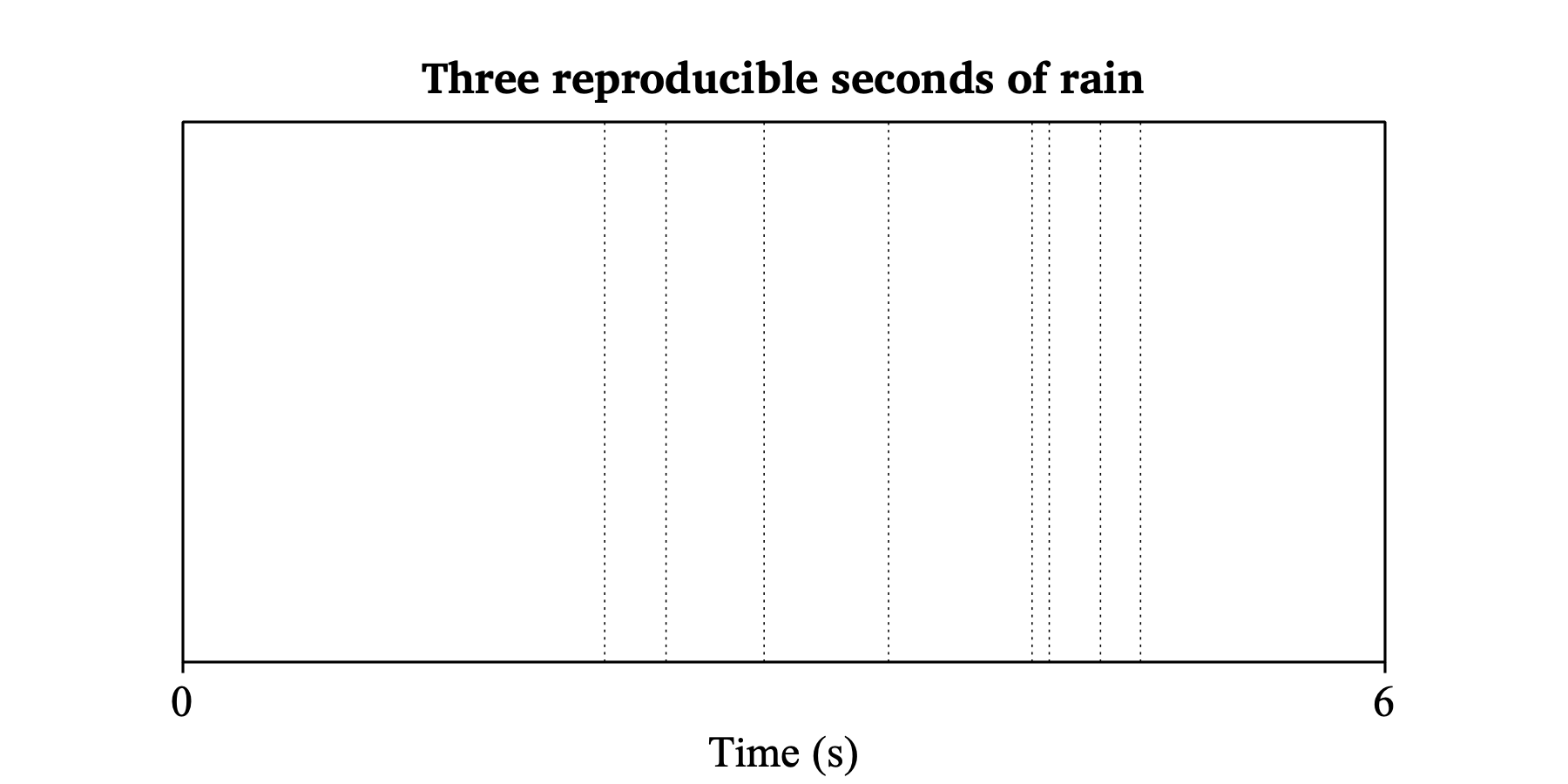
These are only 8 points, and their times will not change when you click “> 1” followed by “1 <”, because Praat’s random generator is initialized to a fixed state, determined by the arbitrary number 1234567654321 (you can use any number you like, with different results depending on that number) in the first line of the script.

To replicate how these 8 numbers were created, we first replicate their count:

We then replicate the actual times according to the algorithm above:

In a PointProcess, these 8 points will be in sorted order:

Here you can see, as in the picture, that the interval between the 4th and 5th point is the largest, and the interval between the 5th and 6th point is the smallest.

We can add these eight points at one stroke to an empty PointProcess:

Slow implementation

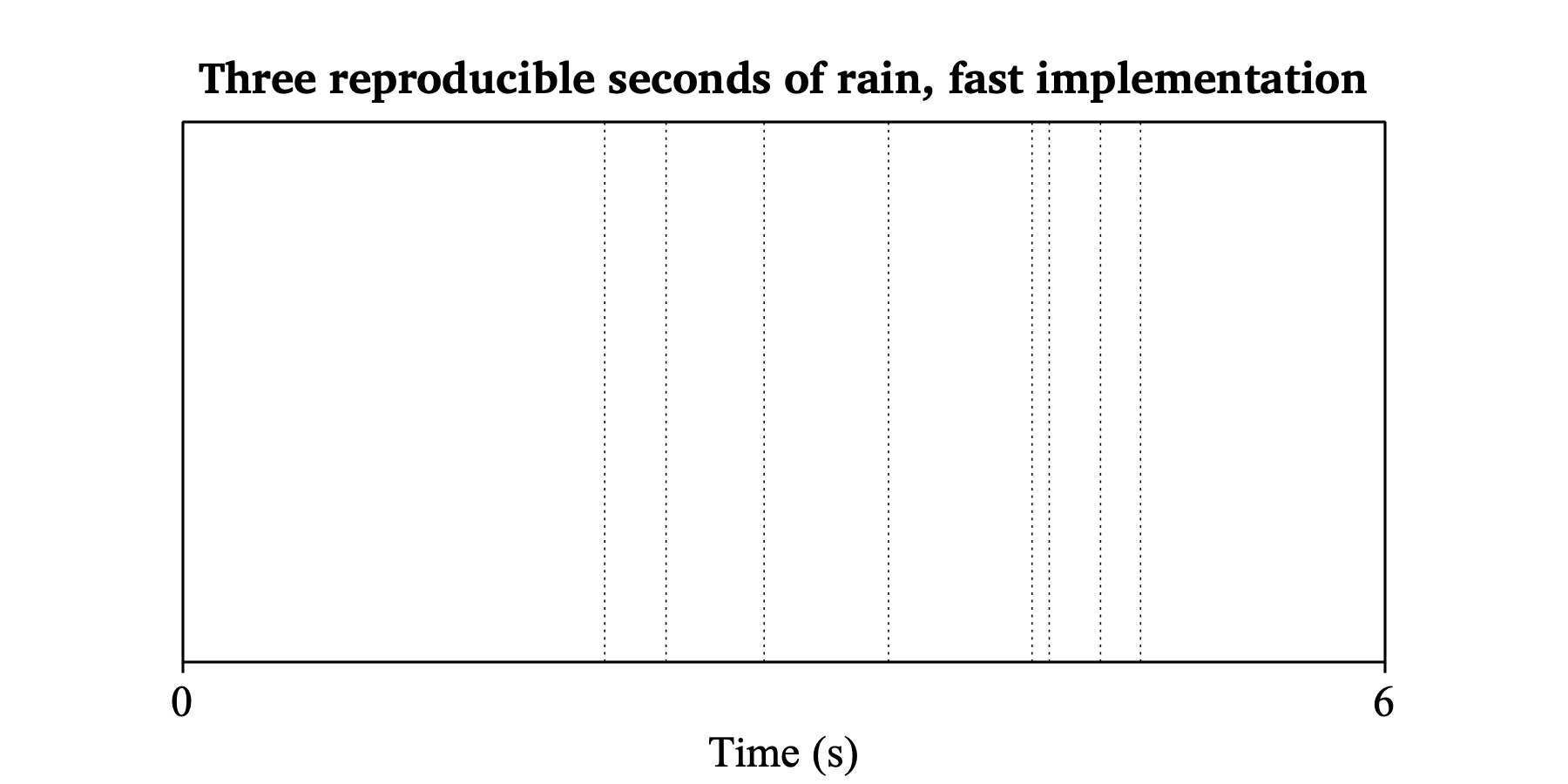
We could also have generated the eight points one by one, and added them immediately to an empty PointProcess:

This is slower than the fast implementation, because of two causes:

(1) the for-loop shown in the Praat script above is slower than the for-loop in the C++ implementation of Add points....

(2) every call to Add point... causes the new point to be inserted into an existing array of points, so the complexity of the whole procedure is O(N²) (as the complexity of insertion is O(N)), while Add points... adds all new points to the end of the existing array (O(N · log N)), then sorts the new array just once, which is again O(N · log N).

Links to this page

• New menu