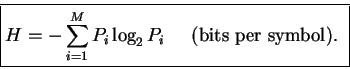>

Information Theory Primer
With an Appendix on Logarithms
Postscript version: ftp://ftp.ncifcrf.gov/pub/delila/primer.ps
web versions: http://www.lecb.ncifcrf.gov/$\sim$toms/paper/primer/

Thomas D. Schneider¹

version = 2.54 of primer.tex 2003 Jan 6

This primer is written for molecular biologists who are unfamiliar with information theory. Its purpose is to introduce you to these ideas so that you can understand how to apply them to binding sites [1,2,3,4,5,6,7,8,9]. Most of the material in this primer can also be found in introductory texts on information theory. Although Shannon's original paper on the theory of information [10] is sometimes difficult to read, at other points it is straight forward. Skip the hard parts, and you will find it enjoyable. Pierce later published a popular book [11] which is a great introduction to information theory. Other introductions are listed in reference [1]. A workbook that you may find useful is reference [12]. Shannon's complete collected works have been published [13]. Information about ordering this book is given in

http://www.lecb.ncifcrf.gov/$\sim$toms/bionet.info-theory.faq.html
#REFERENCES-Information_Theory

Other papers and documentation on programs can be found at

http://www.lecb.ncifcrf.gov/$\sim$toms/

Note: If you have trouble getting through one or more steps in this primer, please send email to me describing the exact place(s) that you had the problem. If it is appropriate, I will modify the text to smooth the path. My thanks go to the many people whose stubbed toes led to this version.

Information and Uncertainty

Information and uncertainty are technical terms that describe any process that selects one or more objects from a set of objects. We won't be dealing with the meaning or implications of the information since nobody knows how to do that mathematically. Suppose we have a device that can produce 3 symbols, A, B, or C. As we wait for the next symbol, we are uncertain as to which symbol it will produce. Once a symbol appears and we see it, our uncertainty decreases, and we remark that we have received some information. That is, information is a decrease in uncertainty. How should uncertainty be measured? The simplest way would be to say that we have an ``uncertainty of 3 symbols''. This would work well until we begin to watch a second device at the same time, which, let us imagine, produces symbols 1 and 2. The second device gives us an ``uncertainty of 2 symbols''. If we combine the devices into one device, there are six possibilities, A1, A2, B1, B2, C1, C2. This device has an ``uncertainty of 6 symbols''. This is not the way we usually think about information, for if we receive two books, we would prefer to say that we received twice as much information than from one book. That is, we would like our measure to be additive.

It's easy to do this if we first take the logarithm of the number of possible symbols because then we can add the logarithms instead of multiplying the number of symbols. In our example, the first device makes us uncertain by $\log(3)$, the second by $\log(2)$ and the combined device by $\log(3)+\log(2)=\log(6)$. The base of the logarithm determines the units. When we use the base 2 the units are in bits (base 10 gives digits and the base of the natural logarithms, e, gives nats [14] or nits, though I don't have a reference for the latter). Thus if a device produces one symbol, we are uncertain by $\log_2 1 = 0$ bits, and we have no uncertainty about what the device will do next. If it produces two symbols our uncertainty would be $\log_2 2 = 1$ bit. In reading an mRNA, if the ribosome encounters any one of 4 equally likely bases, then the uncertainty is 2 bits.

So far, our formula for uncertainty is $\log_2 ( M )$, with M being the number of symbols. The next step is to extend the formula so it can handle cases where the symbols are not equally likely. For example, if there are 3 possible symbols, but one of them never appears, then our uncertainty is 1 bit. If the third symbol appears rarely relative to the other two symbols, then our uncertainty should be larger than 1 bit, but not as high as $\log_2(3)$ bits. Let's begin by rearranging the formula like this:

$$\log_2 ( M ) - \log_2 ( M^{-1} )$$ = (1)

$$- \log_2 ( \frac{1}{M} )$$ =

$$- \log_2 ( P )$$ =

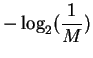so that P = 1/M is the probability that any symbol appears. (If you don't remember this trick of `pulling the sign out', recall that $\log M^b = b \log M$ and let b = -1.)

Now let's generalize this for various probabilities of the symbols, P_i, so that the probabilities sum to 1:

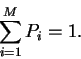$$\sum_{i = 1}^M P_i = 1 .$$ (2)

(Recall that the $\sum$ symbol means to add the P_i together, for i starting at 1 and ending at M.) The surprise that we get when we see the i^th kind of symbol was called the ``surprisal'' by Tribus [15] and is defined by analogy with $- \log_2 P$ to be:

$$u_i = - \log_2 ( P_i ) .$$ (3)

For example, if P_i approaches 0, then we will be very surprised to see the i^th symbol (since it should almost never appear), and the formula says u_i approaches $\infty$. On the other hand, if P_i=1, then we won't be surprised at all to see the i^th symbol (because it should always appear) and u_i = 0.

Uncertainty is the average surprisal for the infinite string of symbols produced by our device. For the moment, let's find the average for a string of only N symbols. Suppose that the i^th type symbol appears N_i times so that

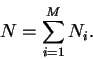$$N = \sum_{i = 1}^M N_i .$$ (4)

There will be N_i cases where we have surprisal u_i. The average surprisal for the N symbols is:

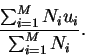$$\frac {\sum_{i = 1}^M N_i u_i} {\sum_{i = 1}^M N_i} .$$ (5)

By substituting N for the denominator and bringing it inside the upper sum, we obtain:

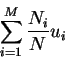$${\sum_{i = 1}^M {\frac{N_i}{N}} u_i}$$ (6)

If we do this measure for an infinite string of symbols, then the frequency N_i / N becomes P_i, the probability of the i^th symbol. Making this substitution, we see that our average surprisal (H) would be:

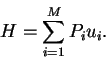$$H = \sum_{i = 1}^M P_i u_i .$$ (7)

Finally, by substituting for u_i, we get Shannon's famous general formula for uncertainty:

$$\framebox{$\displaystyle H = - \sum_{i = 1}^M P_i \log_2 P_i \;\;\;\;\;\mbox{(bits per symbol).} $ }$$ (8)

Shannon got to this formula by a much more rigorous route than we did, by setting down several desirable properties for uncertainty, and then deriving the function. Hopefully the route we just followed gives you a feeling for how the formula works.

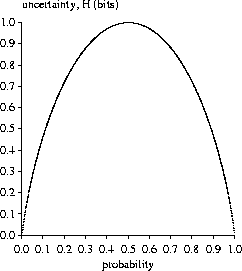
To see how the H function looks, we can plot it for the case of two symbols. This is shown below²:

Notice that the curve is symmetrical, and rises to a maximum when the two symbols are equally likely (probability = 0.5). It falls towards zero whenever one of the symbols becomes dominant at the expense of the other symbol.

As an instructive exercise, suppose that all the symbols are equally likely. What does the formula for H (equation (8)) reduce to? You may want to try this yourself before reading on.

*********************************

Equally likely means that P_i = 1/M, so if we substitute this into the uncertainty equation we get:

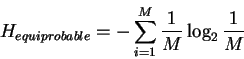$$H_{equiprobable} = - \sum_{i = 1}^M \frac{1}{M} \log_2 \frac{1}{M}$$ (9)

Since M is not a function of i, we can pull it out of the sum:

$$- ( \frac{1}{M} \log_2 \frac{1}{M} ) \sum_{i = 1}^M 1$$ H_equiprobable = 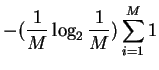(10)

$$- \left( \frac{1}{M} \log_2 {\frac{1}{M}} \right) M$$ =

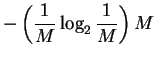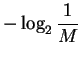$$- \log_2 \frac{1}{M}$$ = (11)

$$\log_2 M$$ =

which is the simple equation we started with. It can be shown that for a given number of symbols (ie., M is fixed) the uncertainty H has its largest value only when the symbols are equally probable. For example, an unbiased coin is harder to guess than a biased coin. As another exercise, what is the uncertainty when there are 10 symbols and only one of them appears? (clue: $$\lim_{p \rightarrow 0} p \log p = 0$$ by setting p = 1/Mand using l'Hôpital's rule, so $0 \log_2 0 = 0$.)

What does it mean to say that a signal has 1.75 bits per symbol? It means that we can convert the original signal into a string of 1's and 0's (binary digits), so that on the average there are 1.75 binary digits for every symbol in the original signal. Some symbols will need more binary digits (the rare ones) and others will need fewer (the common ones). Here's an example. Suppose we have M = 4 symbols:

$$A \;\;\;\;\; C \;\;\;\;\; G \;\;\;\;\; T$$ (12)

with probabilities (P_i):

$$P_A = \frac{1}{2} , \;\;\;\;\; P_C = \frac{1}{4} , \;\;\;\;\; P_G = \frac{1}{8} , \;\;\;\;\; P_T = \frac{1}{8} ,$$ (13)

which have surprisals ( $- \log_2 P_i$):

$$u_A = 1 \mbox{ bit}, \;\;\;\;\; u_C = 2 \mbox{ bits}, \;\;\;\;\; u_G = 3 \mbox{ bits}, \;\;\;\;\; u_T = 3 \mbox{ bits},$$ (14)

so the uncertainty is

$$H = \frac{1}{2} \cdot 1 + \frac{1}{4} \cdot 2 + \frac{1}{8... ...t 3 + \frac{1}{8} \cdot 3 = 1.75 \mbox{ (bits per symbol)} .$$ (15)

Let's recode this so that the number of binary digits equals the surprisal:

 

A = 1

C = 01

G = 000

T = 001 (16)

so the string

ACATGAAC (17)

which has frequencies the same as the probabilities defined above, is coded as

10110010001101 . (18)

14 binary digits were used to code for 8 symbols, so the average is 14/8 = 1.75 binary digits per symbol. This is called a Fano code. Fano codes have the property that you can decode them without needing spaces between symbols. Usually one needs to know the ``reading frame'', but in this example one can figure it out. In this particular coding (equations (16)), the first binary digit distinguishes between the set containing A, (which we symbolize as A) and the set C, G, T, which are equally likely. The second digit, used if the first digit is 0, distinguishes C from G, T. The final digit distinguishes G from T. Because each choice is equally likely (in our original definition of the probabilities of the symbols), every binary digit in this code carries 1 bit of information. Beware! This won't always be true. A binary digit can supply 1 bit only if the two sets represented by the digit are equally likely (as rigged for this example). If they are not equally likely, one binary digit supplies less than one bit. (Recall that H is at a maximum for equally likely probabilities.) So if the probabilities were

$$P_A = \frac{1}{2}, \;\;\;\;\; P_C = \frac{1}{6}, \;\;\;\;\; P_G = \frac{1}{6}, \;\;\;\;\; P_T = \frac{1}{6},$$ (19)

there is no way to assign a (finite) code so that each binary digit has the value of one bit (by using larger blocks of symbols, one can approach it). In the rigged example, there is no way to use fewer than 1.75 binary digits per symbol, but we could be wasteful and use extra digits to represent the signal. The Fano code does reasonably well by splitting the symbols into successive groups that are equally likely to occur; you can read more about it in texts on information theory. The uncertainty measure tells us what could be done ideally, and so tells us what is impossible. For example, the signal with 1.75 bits per symbol could not be coded using only 1 binary digit per symbol.

Tying the Ideas Together

In the beginning of this primer we took information to be a decrease in uncertainty. Now that we have a general formula for uncertainty, (8), we can express information using this formula. Suppose that a computer contains some information in its memory. If we were to look at individual flip-flops, we would have an uncertainty H_before bits per flip-flop. Suppose we now clear part of the computer's memory (by setting the values there to zero), so that there is a new uncertainty, smaller than the previous one: H_after. Then the computer memory has lost an average of

 

R = H_before - H_after (20)

bits of information per flip-flop. If the computer was completely cleared, then H_after = 0 and R = H_before.

Now consider a teletype receiving characters over a phone line. If there were no noise in the phone line and no other source of errors, the teletype would print the text perfectly. With noise, there is some uncertainty about whether a character printed is really the right one. So before a character is printed, the teletype must be prepared for any of the letters, and this prepared state has uncertainty H_before, while after each character has been received there is still some uncertainty, H_after. This uncertainty is based on the probability that the symbol that came through is not equal to the symbol that was sent, and it measures the amount of noise.

Shannon gave an example of this in section 12 of [10] (pages 33-34 of [13]). A system with two equally likely symbols transmitting every second would send at a rate of 1 bit per second without errors. Suppose that the probability that a 0 is received when a 0 is sent is 0.99 and the probability of a 1 received is 0.01. ``These figures are reversed if a 1 is received.'' Then the uncertainty after receiving a symbol is $H_{after} = - 0.99 \log_2 0.99 - 0.01 \log_2 0.01 = 0.081$, so that the actual rate of transmission is R = 1 - 0.081 = 0.919 bits per second.³ The amount of information that gets through is given by the decrease in uncertainty, equation (20).

Unfortunately many people have made errors because they did not keep this point clear. The errors occur because people implicitly assume that there is no noise in the communication. When there is no noise, R = H_before, as with the completely cleared computer memory. That is if there is no noise, the amount of information communicated is equal to the uncertainty before communication. When there is noise and someone assumes that there isn't any, this leads to all kinds of confusing philosophies. One must always account for noise.

One Final Subtle Point. In the previous section you may have found it odd that I used the word ``flip-flop''. This is because I was intentionally avoiding the use of the word ``bit''. The reason is that there are two meanings to this word, as we mentioned before while discussing Fano coding, and it is best to keep them distinct. Here are the two meanings for the word ``bit'':

1.

A binary digit, 0 or 1. This can only be an integer. These `bits' are the individual pieces of data in computers.

2.

A measure of uncertainty, H, or information R. This can be any real number because it is an average. It's the measure that Shannon used to discuss communication systems.