|
A command available in the Combine menu when you select two Sound objects. This command convolves two selected Sound objects with each other. As a result, a new Sound will appear in the list of objects; this new Sound is the convolution of the two original Sounds.
The convolution f*g of two continuous time signals f(t) and g(t) is defined as the integral
| (f*g) (t) ≡ ∫ f(τ) g(t−τ) dτ |
If f and g are sampled signals (as Sounds are in Praat), with the same sampling period Δt, the definition is discretized as
| (f*g) [t] ≡ ∑τ f[τ] g[t−τ] Δt |
where τ and t-τ are the discrete times at which f and g are defined, respectively.
Convolution is a commutative operation, i.e. g*f equals f*g. This means that the order in which you put the two Sounds in the object list does not matter: you get the same result either way.
You can see in the formula above that if both input Sounds are expressed in units of Pa, the resulting Sound should ideally be expressed in Pa2s. Nevertheless, Praat will express it in Pa, because Sounds cannot be expressed otherwise.
This basically means that it is impossible to get the amplitude of the resulting Sound correct for all purposes. For this reason, Praat considers a different definition of convolution as well, namely as the sum
| (f*g) [t] ≡ ∑τ f[τ] g[t−τ] |
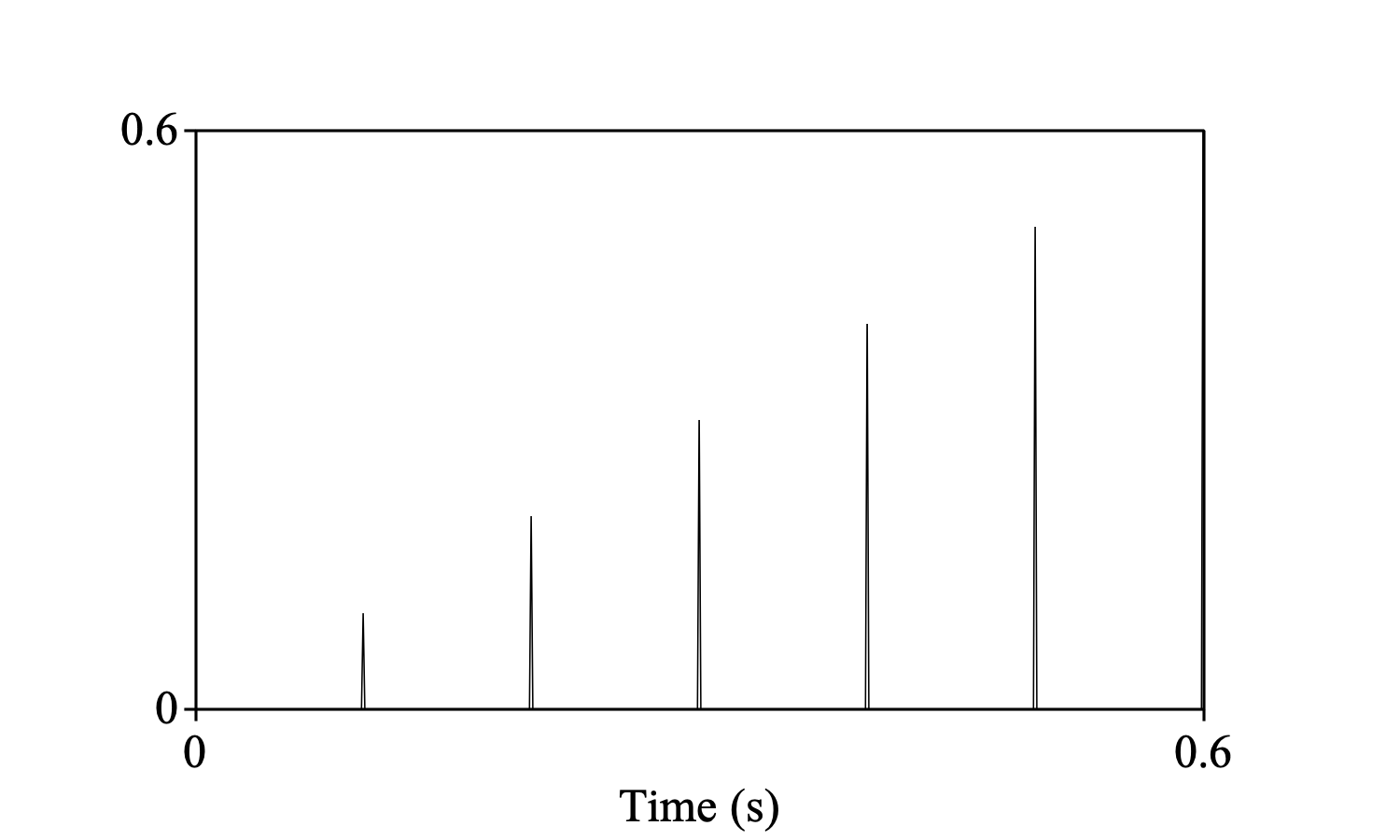
The sum definition is appropriate if you want to filter a pulse train with a finite-impulse-response filter and expect the amplitudes of each resulting period to be equal to the amplitude of the filter. Thus, the pulse train
Create Sound from formula: "peaks", 1, 0.0, 0.6, 1000, ~ x * (col mod 100 = 0)
Draw: 0, 0, 0.0, 0.6, "yes", "curve"

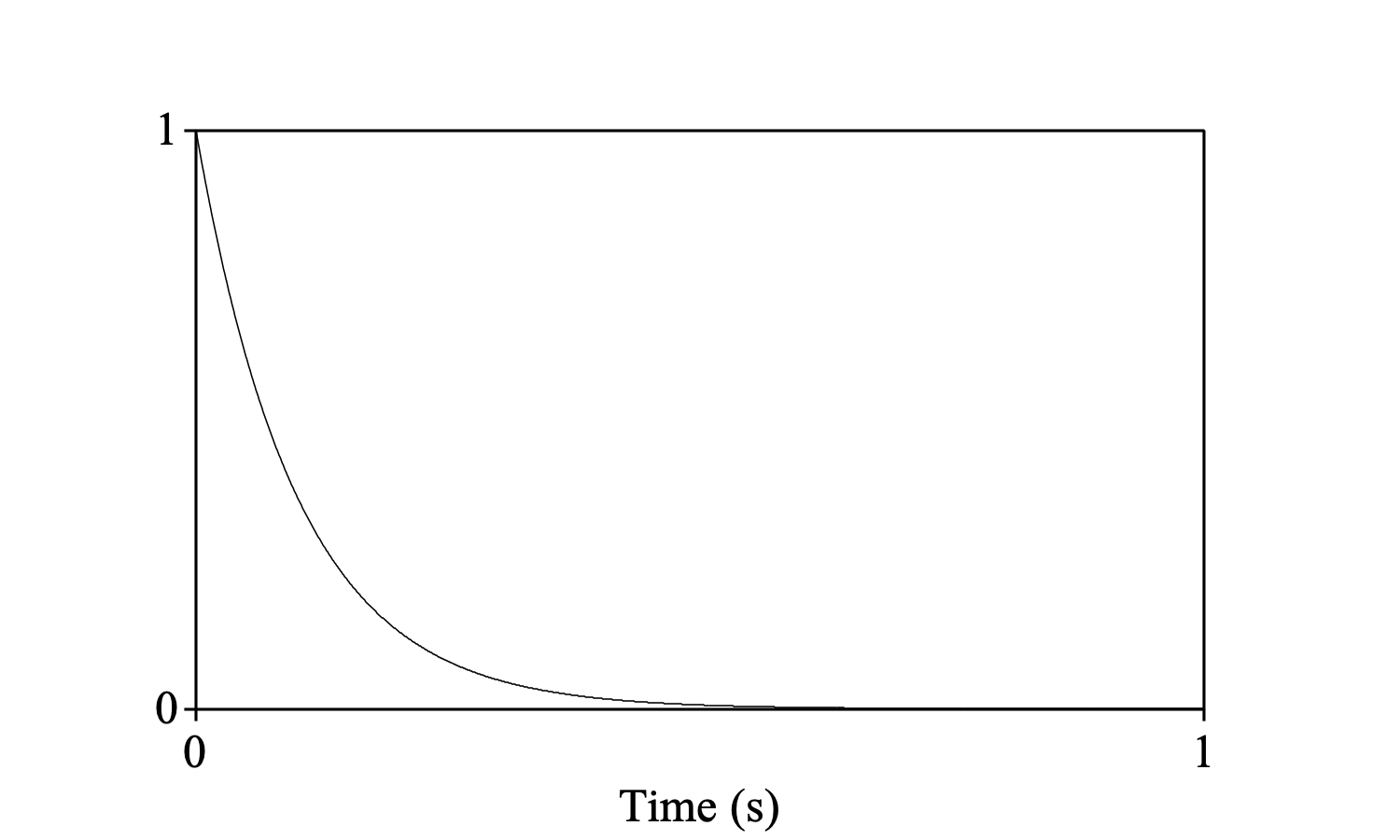
convolved with the “leaky integrator” filter
Create Sound from formula: "leak", 1, 0.0, 1.0, 1000, ~ exp (-x / 0.1)
Draw: 0, 0, 0.0, 1.0, "yes", "curve"
yields the convolution
selectObject: "Sound peaks", "Sound leak"
Convolve: "sum", "zero"
Draw: 0, 0, 0.0, 0.8523, "yes", "curve"
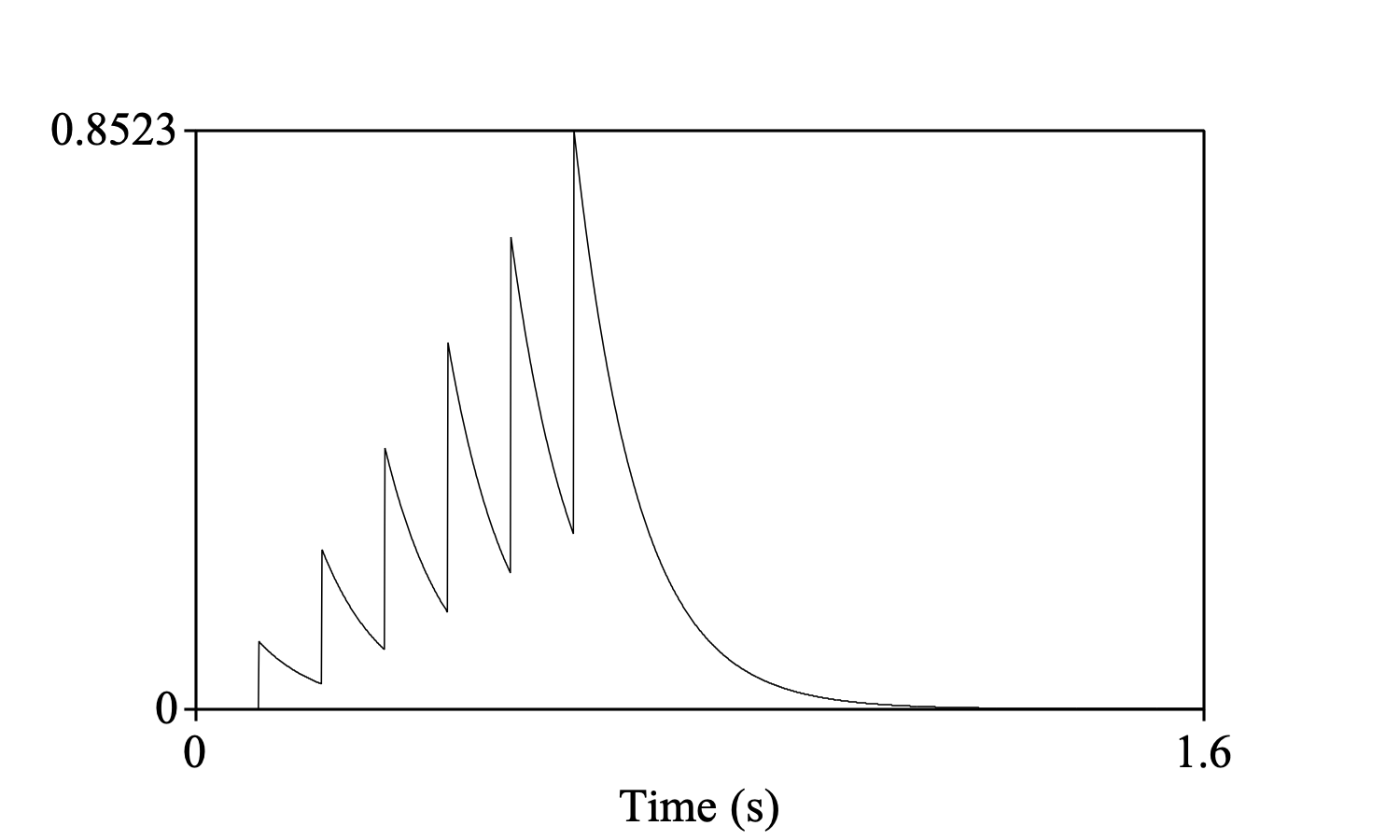
The difference between the integral and sum definitions is that in the sum definition the resulting sound is divided by Δt.
The normalized convolution is defined as
| (normalized f*g) (t) ≡ ∫ f(τ) g(t−τ) dτ / √ (∫ f2(τ) dτ ∫ g2(τ) dτ) |
The boundaries of the integral in 1 are −∞ and +∞. However, f and g are Sound objects in Praat and therefore have finite time domains. If f runs from t1 to t2 and is assumed to be zero before t1 and after t2, and g runs from t3 to t4 and is assumed to be zero outside that domain, then the convolution will be zero before t1+t3 and after t2+t4, while between t1+t3 and t2+t4 it is
| (f*g) (t) = ∫t1t2 f(τ) g(t−τ) dτ |
In this formula, the argument of f runs from t1 to t2, but the argument of g runs from (t1+t3)−t2 to (t2+t4)−t1, i.e. from t3−(t2−t1) to t4+(t2−t1). This means that the integration is performed over two equal stretches of time during which g must be taken zero, namely a time stretch before t3 and a time stretch after t4, both of duration t2−t1 (equivalent equations can be formulated that rely on two stretches of t4−t3 of zeroes in f rather than in g, or on a stretch of t2−t1 of zeroes in g and a stretch of t4−t3 of zeroes in f.
If you consider the sounds outside their time domains as similar to what they are within their time domains, instead of zero, the discretized formula in 1 should be based on the average over the jointly defined values of f[τ] and g[t−τ], without counting any multiplications of values outside the time domains. Suppose that f is defined on the time domain [0, 1.2] with the value of 1 everywhere, and g is defined on the time domain [0, 3] with the value 1 everywhere. Their convolution under the assumption that they are zero elsewhere is then
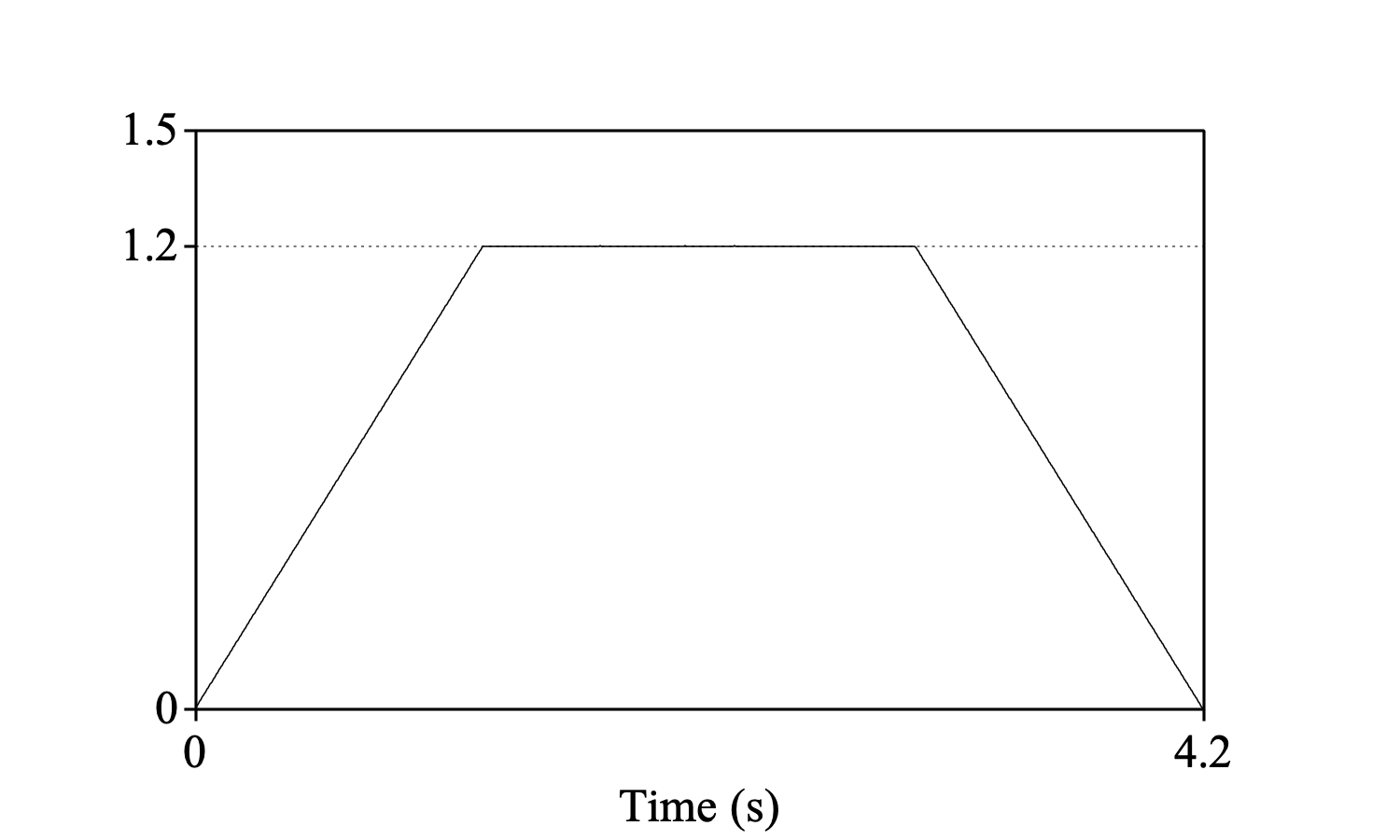
but under the assumption that the sounds are similar (i.e. 1) elsewhere, their convolution should be
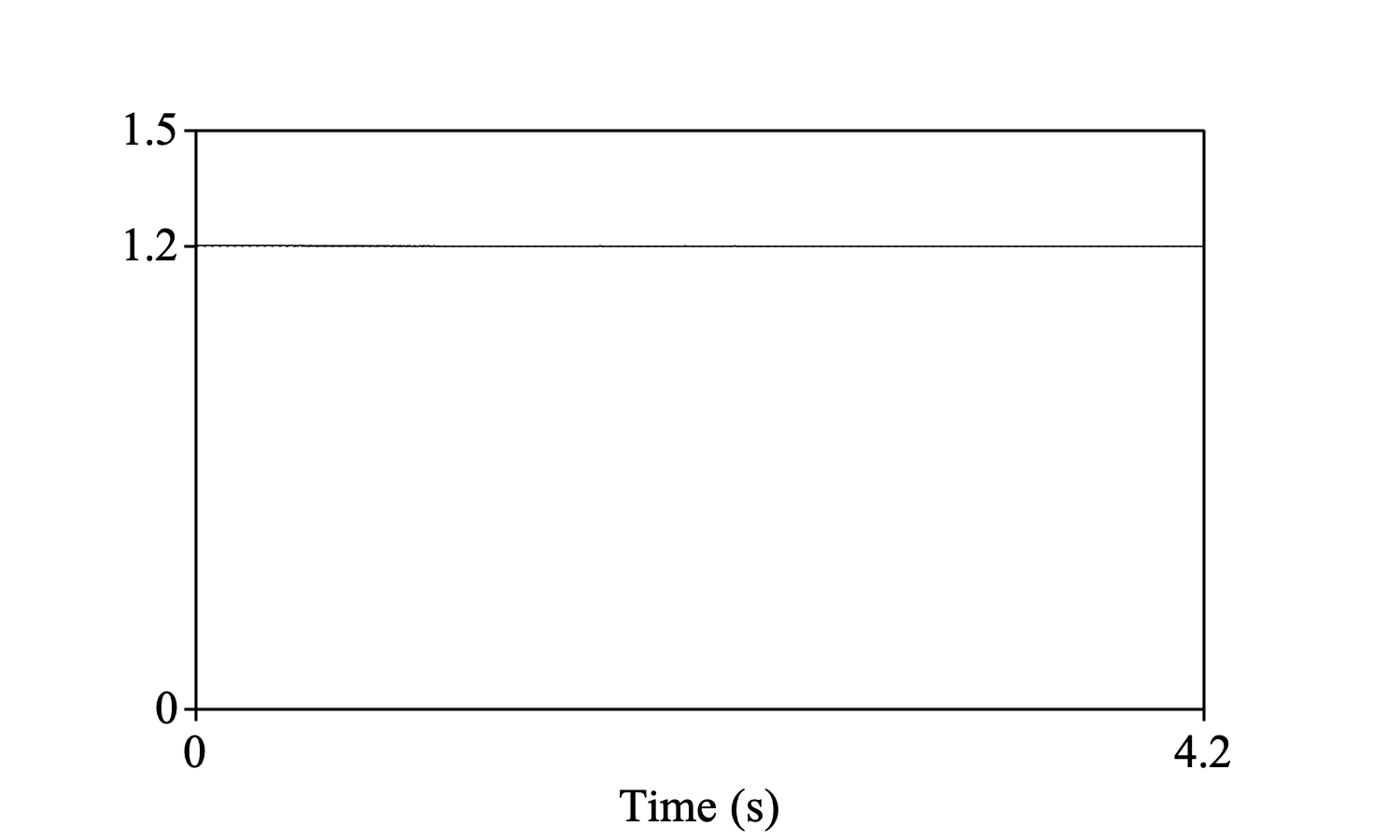
i.e. a constant value of 1.2. This is what you get by choosing the similar option; if f is shorter than g, the first and last parts of the convolution will be divided by a straight line of duration t2−t1 to compensate for the fact that the convolution has been computed over fewer values of f and g there.
The start time of the resulting Sound will be the sum of the start times of the original Sounds, the end time of the resulting Sound will be the sum of the end times of the original Sounds, the time of the first sample of the resulting Sound will be the sum of the first samples of the original Sounds, the time of the last sample of the resulting Sound will be the sum of the last samples of the original Sounds, and the number of samples in the resulting Sound will be the sum of the numbers of samples of the original Sounds minus 1.
You can convolve e.g. a 10-channel sound either with another 10-channel sound or with a 1-channel (mono) sound.
If both Sounds have more than one channel, the two Sounds have to have the same number of channels; each channel of the resulting Sound is then computed as the convolution of the corresponding channels of the original Sounds. For instance, if you convolve two 10-channel sounds, the resulting sound will have 10 channels, and its 9th channel will be the convolution of the 9th channels of the two original sounds.
If one of the original Sounds has multiple channels and the other Sound has only one channel, the resulting Sound will have multiple channels; each of these is computed as the convolution of the corresponding channel of the multiple-channel original and the single channel of the single-channel original. For instance, if you convolve a 10-channel sound with a mono sound, the resulting sound will have 10 channels, and its 9th channel will be the convolution of the mono sound with the 9th channel of the original 10-channel sound.
The amplitude scaling factor will be the same for all channels, so that the relative amplitude of the channels will be preserved in the resulting sound. For the normalize scaling, for instance, the norm of f in the formula above is taken over all channels of f. For the peak 0.99 scaling, the resulting sound will typically have an absolute peak of 0.99 in only one channel, and lower absolute peaks in the other channels.
The computation makes use of the fact that convolution in the time domain corresponds to multiplication in the frequency domain: we first pad f with a stretch of t4−t3 of zeroes and g with a stretch of t2−t1 of zeroes (see 4 above), so that both sounds obtain a duration of (t2−t1)+(t4−t3); we then calculate the spectra of the two zero-padded sounds by Fourier transformation, then multiply the two spectra with each other, and finally Fourier-transform the result of this multiplication back to the time domain; the result will again have a duration of (t2−t1)+(t4−t3).
© Paul Boersma & David Weenink 2010-04-04,2024