|
OT learning 4. Learning an ordinal grammar
|
|
With the data from a tongue-root-harmony language with five completely ranked constraints, we can have a throw at learning this language, starting with a grammar in which all the constraints are ranked at the same height, or randomly ranked, or with articulatory constraints outranking faithfulness constraints.
Let’s try the third of these. Create an infant tongue-root grammar by choosing Create tongue-root grammar... and specifying “Five” for the constraint set and “Infant” for the ranking. The result after a single evaluation will be like:
-
| ranking value | disharmony | plasticity |
-
| *GESTURE (contour) | 100.000 | 100.631 | 1.000 |
-
| *[atr / lo] | 100.000 | 100.244 | 1.000 |
-
| *[rtr / hi] | 100.000 | 97.086 | 1.000 |
-
| PARSE (rtr) | 50.000 | 51.736 | 1.000 |
-
| PARSE (atr) | 50.000 | 46.959 | 1.000 |
Such a grammar produces all kinds of non-adult results. For instance, the input /ətɪ/ will surface as [atɪ]:
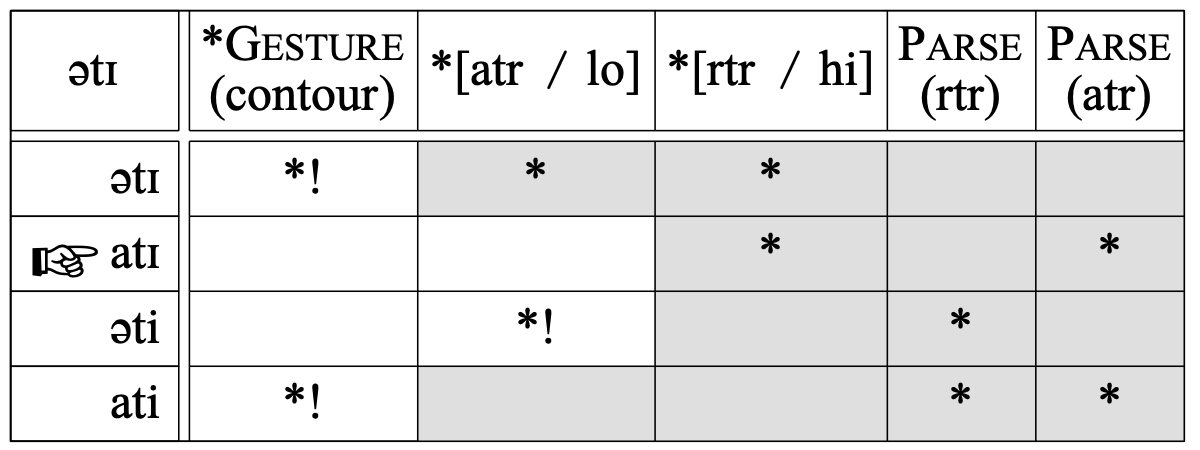
The adult form is very different: [əti]. The cause of the discrepancy is in the order of the constraints *[atr / lo] and *[rtr / hi], which militate against [ə] and [ɪ], respectively. Simply reversing the rankings of these two constraints would solve the problem in this case. More generally, Tesar & Smolensky (1998) claim that demoting all the constraints that cause the adult form to lose into the stratum just below the highest-ranked constraint violated in the learner's form (here, moving *[atr / lo] just below *[rtr / hi] into the same stratum as PARSE (rtr)), will guarantee convergence to the target grammar, if there is no variation in the data (Tesar & Smolensky's algorithm is actually incorrect, but can be repaired easily, as shown by Boersma (2009b)).
But Tesar & Smolensky's algorithm cannot be used for variable data, since all constraints would be tumbling down, exchanging places and producing wildly different grammars at each learning step. Since language data do tend to be variable, we need a gradual and balanced learning algorithm, and the following algorithm is guaranteed to converge to the target language, if that language can be described by a stochastic OT grammar.
The reaction of the learner to hearing the mismatch between the adult [əti] and her own [atɪ], is simply:
- 1. to move the constraints violated in her own form, i.e. *[rtr / hi] and PARSE (atr), up by a small step along the ranking scale, thus decreasing the probability that her form will be the winner at the next evaluation of the same input;
- 2. and to move the constraints violated in the adult form, namely *[atr / lo] and PARSE (rtr), down along the ranking scale, thus increasing the probability that the adult form will be the learner's winner the next time.
If the small reranking step (the plasticity) is 0.1, the grammar will become:
-
| ranking value | disharmony | plasticity |
-
| *GESTURE (contour) | 100.000 | 100.631 | 1.000 |
-
| *[atr / lo] | 99.900 | 100.244 | 1.000 |
-
| *[rtr / hi] | 100.100 | 97.086 | 1.000 |
-
| PARSE (rtr) | 49.900 | 51.736 | 1.000 |
-
| PARSE (atr) | 50.100 | 46.959 | 1.000 |
The disharmonies, of course, will be different at the next evaluation, with a probability slightly higher than 50% that *[rtr / hi] will outrank *[atr / lo]. Thus the relative rankings of these two grounding constraints have moved into the direction of the adult grammar, in which they are ranked at opposite ends of the grammar.
Note that the relative rankings of PARSE (atr) and PARSE (rtr) are now moving in a direction opposite to where they will have to end up in this RTR-dominant language. This does not matter: the procedure will converge nevertheless.
We are now going to simulate the infant who learns simplified Wolof. Take an adult Wolof grammar and generate 1000 input strings and the corresponding 1000 output strings following the procedure described in §3.2. Now select the infant OTGrammar and both Strings objects, and choose Learn.... After you click OK, the learner processes each of the 1000 input-output pairs in succession, gradually changing the constraint ranking in case of a mismatch. The resulting grammar may look like:
-
| ranking value | disharmony | plasticity |
-
| *[rtr / hi] | 100.800 | 98.644 | 1.000 |
-
| *GESTURE (contour) | 89.728 | 94.774 | 1.000 |
-
| *[atr / lo] | 89.544 | 86.442 | 1.000 |
-
| PARSE (rtr) | 66.123 | 65.010 | 1.000 |
-
| PARSE (atr) | 63.553 | 64.622 | 1.000 |
We already see some features of the target grammar, namely the top ranking of *[rtr / hi] and RTR dominance (the mutual ranking of the PARSE constraints). The steps have not been exactly 0.1, because we also specified a relative plasticity spreading of 0.1, thus giving steps typically in the range of 0.7 to 1.3. The step is also multiplied by the constraint plasticity, which is simply 1.000 in all examples in this tutorial; you could set it to 0.0 to prevent a constraint from moving up or down at all. The leak is the part of the constraint weight (especially in Harmonic Grammar) that is thrown away whenever a constraint is reranked; e.g if the leak is 0.01 and the step is 0.11, the constraint weight is multiplied by (1 – 0.01·0.11) = 0.9989 before the learning step is taken; in this way you could implement forgetful learning of correlations.
After learning once more with the same data, the result is:
-
| ranking value | disharmony | plasticity |
-
| *[rtr / hi] | 100.800 | 104.320 | 1.000 |
-
| PARSE (rtr) | 81.429 | 82.684 | 1.000 |
-
| *[atr / lo] | 79.966 | 78.764 | 1.000 |
-
| *GESTURE (contour) | 81.316 | 78.166 | 1.000 |
-
| PARSE (atr) | 77.991 | 77.875 | 1.000 |
This grammar now sometimes produces faithful disharmonic utterances, because the PARSE now often outrank the gestural constraints at evaluation time. But there is still a lot of variation produced. Learning once more with the same data gives:
-
| ranking value | disharmony | plasticity |
-
| *[rtr / hi] | 100.800 | 100.835 | 1.000 |
-
| PARSE (rtr) | 86.392 | 82.937 | 1.000 |
-
| *GESTURE (contour) | 81.855 | 81.018 | 1.000 |
-
| *[atr / lo] | 78.447 | 78.457 | 1.000 |
-
| PARSE (atr) | 79.409 | 76.853 | 1.000 |
By inspecting the first column, you can see that the ranking values are already in the same order as in the target grammar, so that the learner will produce 100 percent correct adult utterances if her evaluation noise is zero. However, with a noise of 2.0, there will still be variation. For instance, the disharmonies above will produce [ata] instead of [ətə] for underlying /ətə/. Learning seven times more with the same data gives a reasonable proficiency:
-
| ranking value | disharmony | plasticity |
-
| *[rtr / hi] | 100.800 | 99.167 | 1.000 |
-
| PARSE (rtr) | 91.580 | 93.388 | 1.000 |
-
| *GESTURE (contour) | 85.487 | 86.925 | 1.000 |
-
| PARSE (atr) | 80.369 | 78.290 | 1.000 |
-
| *[atr / lo] | 75.407 | 74.594 | 1.000 |
No input forms have error rates above 4 percent now, so the child has learned a lot with only 10,000 data, which may be on the order of the number of input data she receives every day.
We could have sped up the learning process appreciably by using a plasticity of 1.0 instead of 0.1. This would have given a comparable grammar after only 1000 data. After 10,000 data, we would have
-
| ranking value | disharmony | plasticity |
-
| *[rtr / hi] | 107.013 | 104.362 | 1.000 |
-
| PARSE (rtr) | 97.924 | 99.984 | 1.000 |
-
| *GESTURE (contour) | 89.679 | 89.473 | 1.000 |
-
| PARSE (atr) | 81.479 | 83.510 | 1.000 |
-
| *[atr / lo] | 73.067 | 72.633 | 1.000 |
With this grammar, all the error rates are below 0.2 percent. We see that crucially ranked constraints will become separated after a while by a gap of about 10 along the ranking scale.
If we have three constraints obligatorily ranked as A >> B >> C in the adult grammar, with ranking differences of 8 between A and B and between B and C in the learner's grammar (giving an error rate of 0.2%), the ranking A >> C has a chance of less than 1 in 100 million to be reversed at evaluation time. This relativity of error rates is an empirical prediction of our stochastic OT grammar model.
Our Harmonic Grammars with constraint noise (Noisy HG) are slightly different in that respect, but are capable of learning a constraint ranking for any language that can be generated from an ordinal ranking. As proved by Boersma & Pater (2016), the same learning rule as was devised for MaxEnt grammars by Jäger (2003) is able to learn all languages generated by nonnoisy HG grammars as well; the GLA, by contrast, failed to converge on 0.4 percent of randomly generated OT languages (failures of the GLA on ordinal grammars were discovered first by Pater (2008)). This learning rule for HG and MaxEnt is the same as the GLA described above, except that the learning step of each constraint is multiplied by the difference of the number of violations of this constraint between the correct form and the incorrect winner; this multiplication is crucial (without it, stochastic gradient ascent is not guaranteed to converge), as was noted by Jäger for MaxEnt. The same procedure for updating weights occurs in Soderstrom, Mathis & Smolensky (2006), who propose an incremental version (formulas 21 and 35d) of the harmony version (formulas 14 and 18) of the learning equation for Boltzmann machines (formula 13). The differences between the three implementations is that in Stochastic OT and Noisy HG the evaluation noise (or temperature) is in the constraint rankings, in MaxEnt it is in the candidate probabilities, and in Boltzmann machines it is in the activities (i.e. the constraint violations). The upate procedure is also similar to that of the perceptron, a neural network invented by Rosenblatt (1962) for classifying continuous inputs.
Links to this page
© ppgb 20190331

