|
Instead of generating input-output pairs directly from a PairDistribution object, you can also generate input forms and their winning outputs from an OTGrammar grammar. Of course, that’s what the language data presented to real children comes from. Our example will be a tongue-root harmony grammar.
Choose Create tongue-root grammar... from the Optimality Theory submenu of the New menu. Set Constraint set to Five, and Ranking to Wolof. Click OK. An object called “OTGrammar Wolof” will appear in the list. Click View & Edit. You will see the following grammar appear in the OTGrammarEditor:
| ranking value | disharmony | plasticity |
| *[rtr / hi] | 100.000 | 100.000 | 1.000 |
| PARSE (rtr) | 50.000 | 50.000 | 1.000 |
| *GESTURE (contour) | 30.000 | 30.000 | 1.000 |
| PARSE (atr) | 20.000 | 20.000 | 1.000 |
| *[atr / lo] | 10.000 | 10.000 | 1.000 |
This simplified Wolof grammar, with five constraints with clearly different rankings, is equivalent to the traditional OT ranking
| *[rtr / hi] >> PARSE (rtr) >> *GESTURE (contour) >> PARSE (atr) >> *[atr / lo] |
These constraints are based on a description of Wolof by Archangeli & Pulleyblank (1994: 225–239). For the meaning of these constraints, see Boersma (1998: 295), or the Create tongue-root grammar... manual page.
For each input, there are four output candidates: the vowel heights will be the same as those in the input, but the tongue-root values of V1 and V2 are varied. For example, for the input [ita] we will have the four candidates [ita], [itə], [ɪta], and [ɪtə].
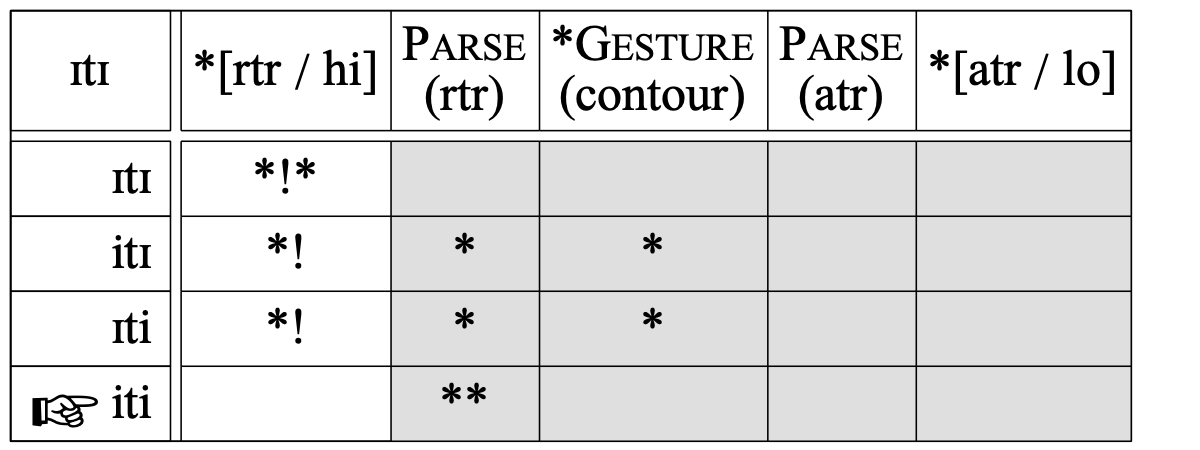
With this way of generating candidates, we see that the five constraints are completely ranked. First, the absolute prohibition on surface [ɪ] shows that *[rtr / hi] outranks RTR faithfulness (otherwise, [ɪtɪ] would have been the winner):

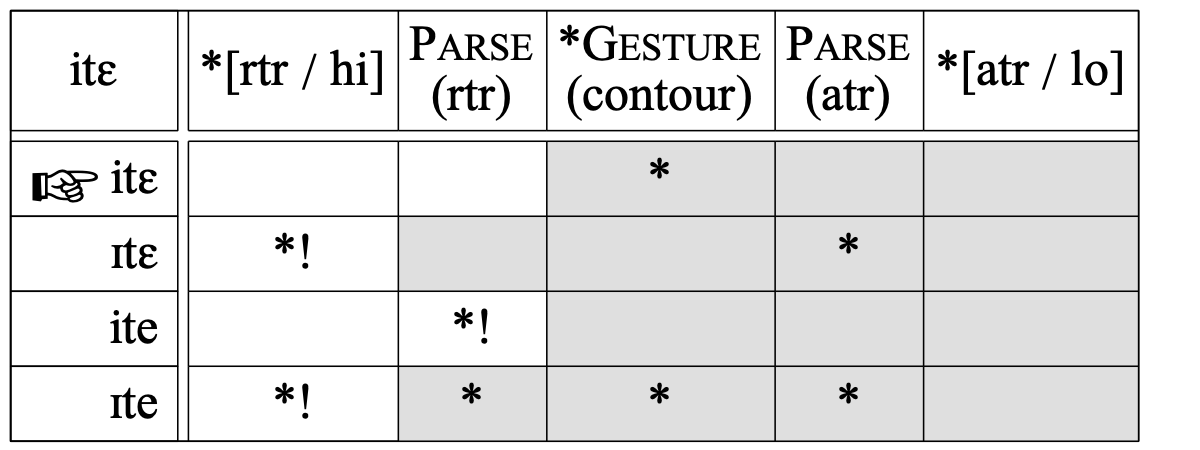
Second, the faithful surfacing of the disharmonic /itɛ/ shows that RTR faithfulness must outrank the harmony (anti-contour) constraint (otherwise, [ite] would have been the winner):
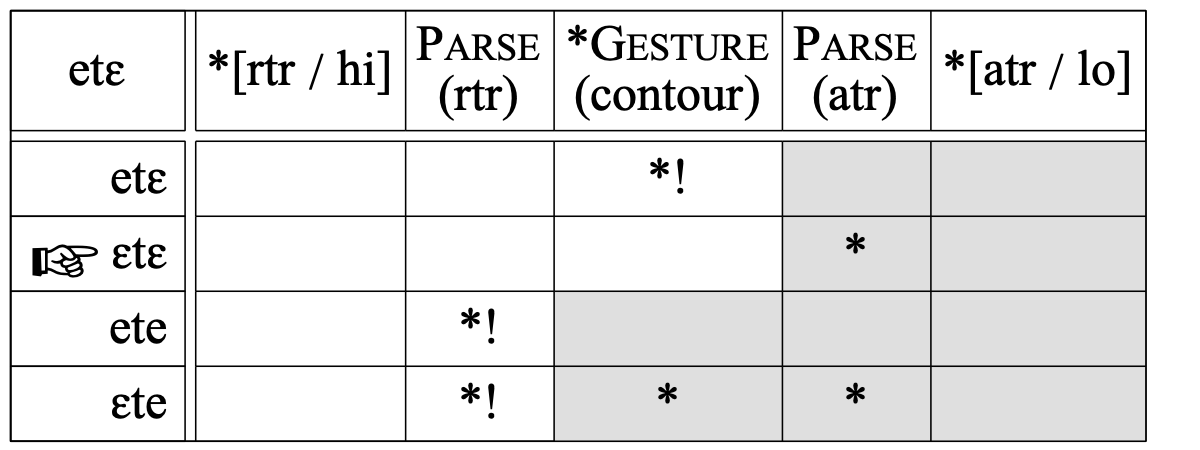
Third, the RTR-dominant harmonicization of underlying disharmonic /etɛ/ shows that harmony must outrank ATR faithfulness (otherwise, [etɛ] would have won):
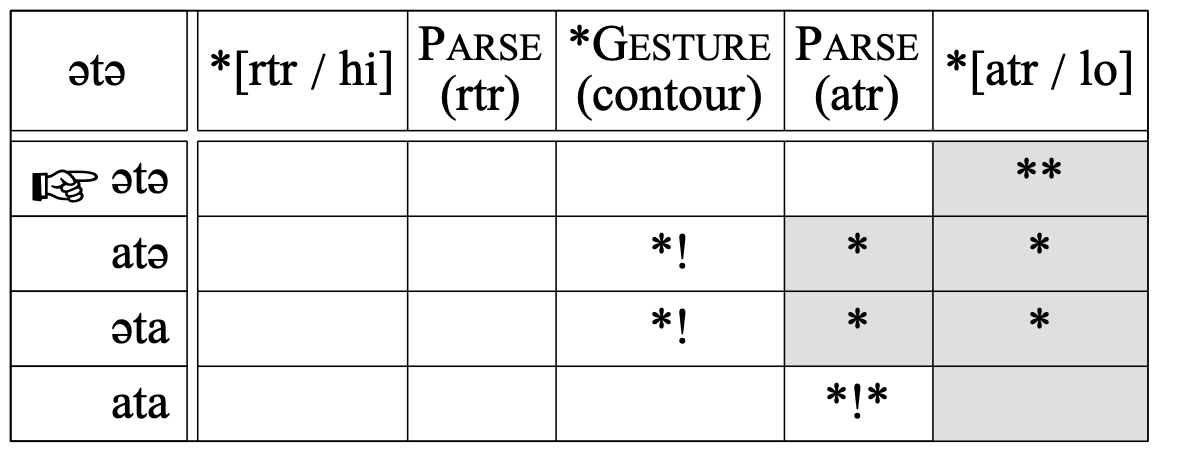
Finally, the faithful surfacing of the low ATR vowel /ə/ even if not forced by harmony, shows that ATR faithfulness outranks *[atr / lo] (otherwise, [ata] would have been the winning candidate):
These four ranking arguments clearly establish the crucial rankings of all five constraints.
According to Prince & Smolensky (1993), the input to an OT grammar can be anything. This is the idea of richness of the base. When doing a practical investigation, however, we are only interested in the inputs that will illustrate the properties of our partial grammars. In the case of simplified Wolof, this means the 36 possible V1tV2 sequences where V1 and V2 are any of the six front vowels i, ɪ, e, ɛ, ə, and a (see Create tongue-root grammar...).
A set of inputs can be generated from an OTGrammar object by inspecting the list of tableaus. So select the Wolof tongue-root grammar and choose Generate inputs.... Set Number of trials to 100, and click OK. A Strings object named Wolof_in will appear in the list. Click Inspect and examine the 100 input strings. You will see that they have been randomly chosen from the 36 possible V1tV2 sequences as described at Create tongue-root grammar...:
| ɛta, etɛ, ɛti, itɛ, ɛtɛ, iti, ɛtɪ, itɪ, ɪti, etɛ, ... |
Thus, when asked to generate a random input, these grammars produce any of the 36 possible V1tV2 sequences, all with equal probability.
To compute the outputs for the above set of input forms, select both the OTGrammar object and the input Strings object, and choose Inputs to outputs..., perhaps specifying zero evaluation noise. A new Strings objects called Wolof_out will appear in the list. If you Inspect it, you will see that it contains a string sequence aligned with the original input strings:
| ɛta, ɛtɛ, ɛti, itɛ, ɛtɛ, iti, ɛti, iti, iti, ɛtɛ, ... |
In this way, we have created two Strings objects, which together form a series of input-output pairs needed for learning a grammar that contains faithfulness constraints.
© ppgb 20110128