How not to eyeball

The solution is: establish your precise analysis procedure before looking at your data, and make that analysis procedure nonselective (e.g. it should not look for the highest peak in the EEG). Your analysis procedure should take into account all possible parts of the data, and correct for multiple possibilities of finding low p-values.

An example is on page 6 by Wanrooij et al. (2014a).

Question: Find a criticism on this part of the paper in the light of Monday’s lecture.

Question: Find a criticism on this part of the paper in the light of Wednesday’s lecture.

Question: Find a criticism on this part of the paper in the light of Wagenmakers et al.’s paper.

Question: what is the solution to this general problem?

What can Bayesian statistics do for you?

• Some people find it better for everything, though Simmons et al. (2011) recommended caution.
• While pre-writing allows you to publish a paper whose main result is a none-result, Bayesian statistics allows you to publish a paper that actually argues for the null hypothesis.

The p-value approach

The p-value approach is based on computing the probability of the observed data, as well as non-observed data, under the null hypothesis.

\[ P (\text{observed or more distant data} \mid H_0) \]

x <- seq (from = -30, to = +30, by = 0.1)
y <- dnorm (x, mean = 0, sd = 8)
plot (x, y, type = "l",
      xlab = "effect", ylab = "probability density",
      ylim = c(-0.005, 0.06))
lines (c(-30, 30), c(0, 0))
lines (c(0, 0), c(0, 0.052))
text (x = 0, y = 0.052, pos = 3, offset = 0.6,
      labels = "null hypothesis")
lines (c(13.5, 13.5), c(0, 0.03))
lines (c(-13.5, -13.5), c(0, 0.03))
text (x = 13.5, y = 0.03, pos = 3, offset = 0.6,
      labels = "observed mean")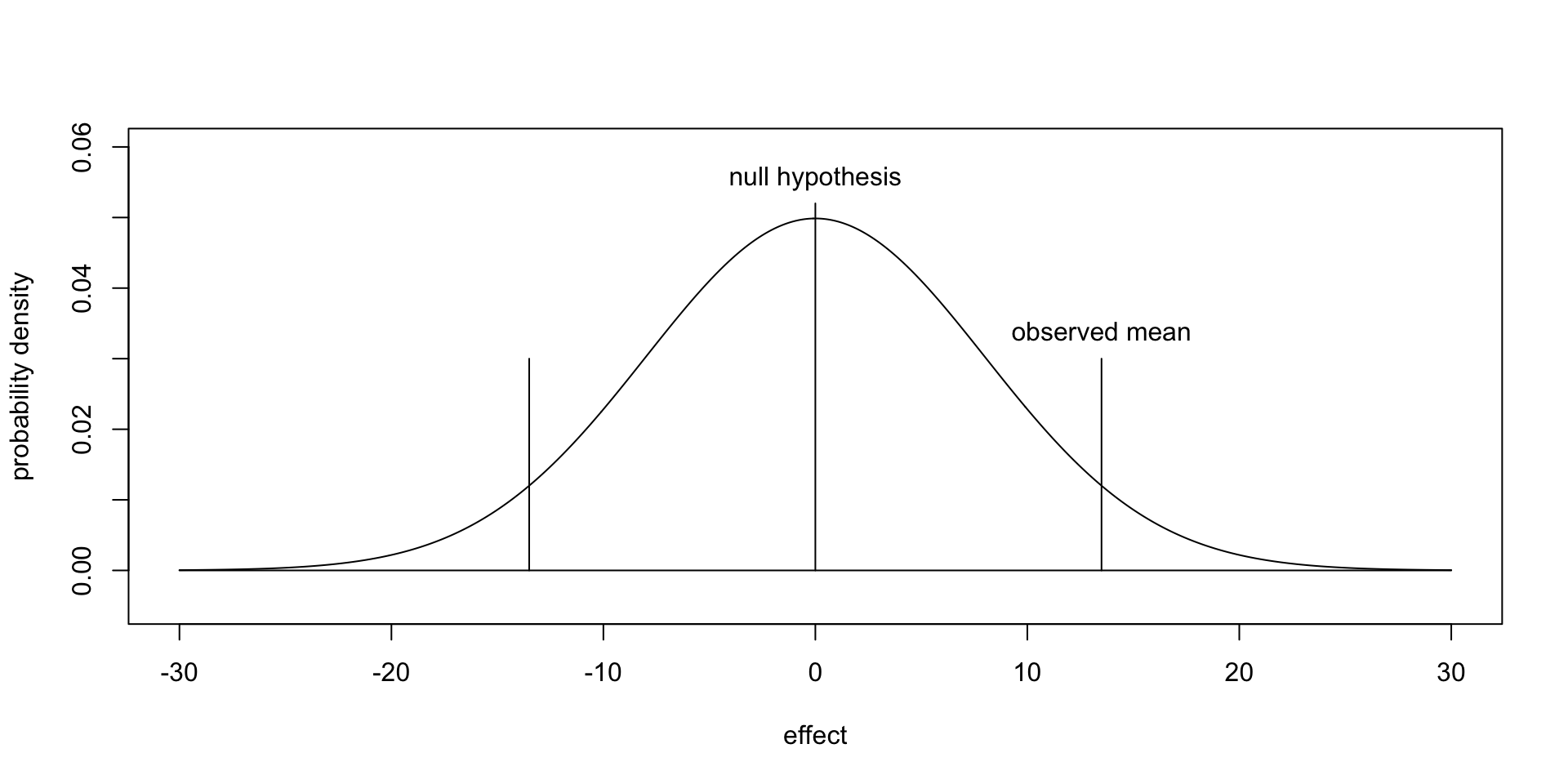

If the standard deviation is known to be 8.0, and the observed mean is 13.5, the p-value is the area under the curve to the right of 13.5, plus the (same) area under the curve to the left of -13.5:

2 * pnorm (13.5, mean = 0.0, sd = 8.0, lower.tail = FALSE)

## [1] 0.09151

The likelihood ratio approach

Suppose you have two hypotheses, H₀ and H₁, and you want to pit them against each other. There is no need for p-value testing, and even no need to compute probability areas of data you have not observed.

For instance, if H₀ is still your null hypothesis (as the name suggests), and H₁ posits that the Flemish are better than the Dutch by 20 along the scale, then H₁ is twice as likely as H₀:

x <- seq (from = -30, to = +30, by = 0.1)
h0 = 0
h1 = 20
y0 <- dnorm (x, mean = h0, sd = 8)
y1 <- dnorm (x, mean = h1, sd = 8)
plot (x, y0, type = "l",
      xlab = "effect", ylab = "probability density",
      ylim = c(-0.005, 0.06))
lines (x, y1)
lines (c(-30, 30), c(0, 0))
lines (c(h0, h0), c(0, 0.052))
lines (c(h1, h1), c(0, 0.052))
text (x = h0, y = 0.052, pos = 3, offset = 0.6,
      labels = "H0")
text (x = h1, y = 0.052, pos = 3, offset = 0.6,
      labels = "H1")
lines (c(13.5, 13.5), c(0, 0.052))
text (x = 13.5, y = 0.052, pos = 3, offset = 0.6,
      labels = "m")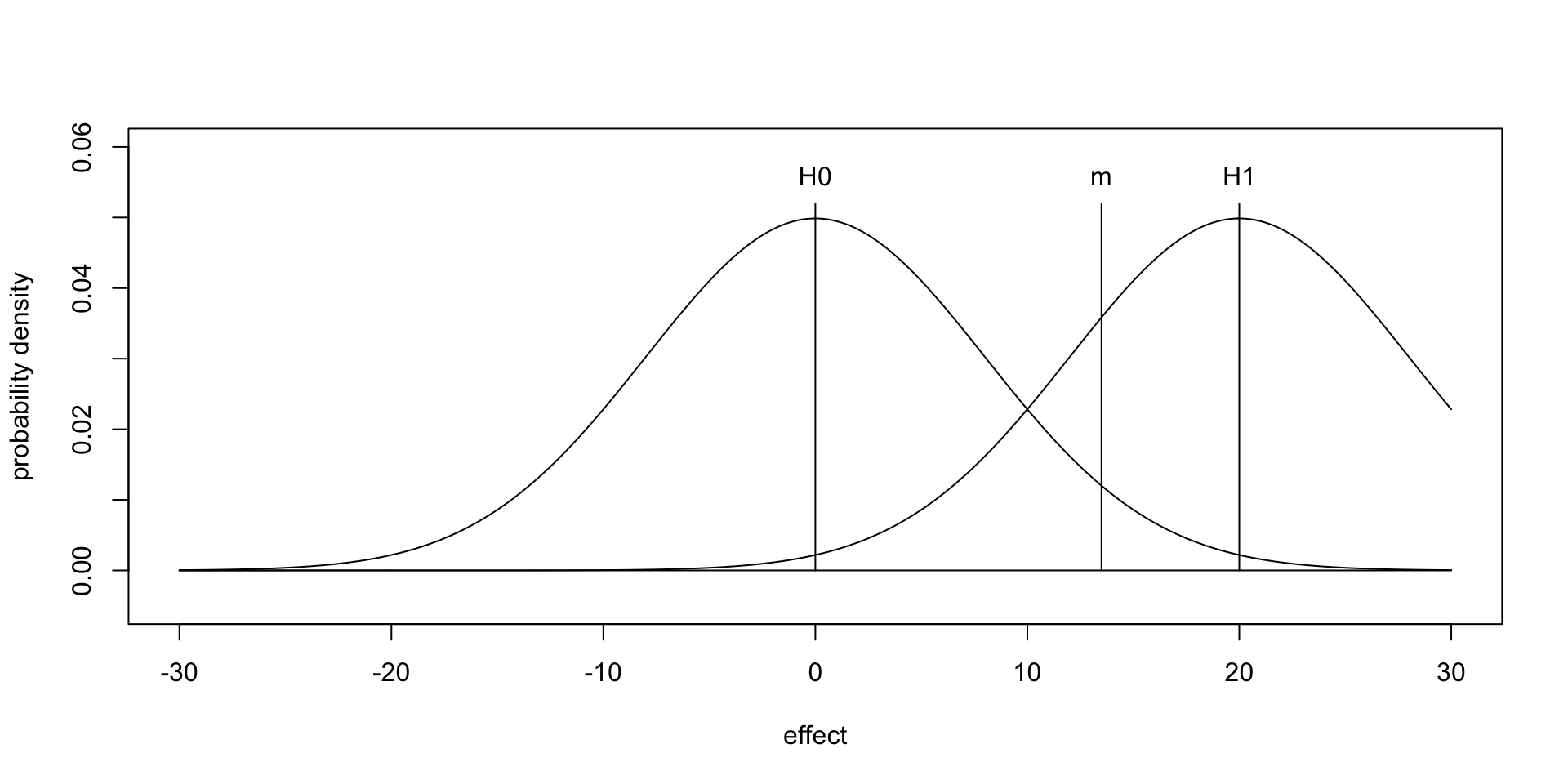

dnorm (13.5, mean=20, sd=8) /dnorm (13.5, mean=0, sd=8)

## [1] 2.985

So the observed data are almost 3 times as likely under H₁ than under H₀.

The likelihood ratio of the data with respect to these two hypotheses is therefore given by

\[ \frac { P (data \mid H_1) }{ P (data \mid H_0) } \]

I here stop talking about likelihood ratios; for today they are just an ingredient for Bayesian reasoning.

The Bayesian approach

Bayesians do not want to know probabilities of the data given any hypothesis, but they want to know the “probability” that a hypothesis is true, i.e. they want to know what odds they can gamble for!

So Bayesians take seriously the existence of a probability of a hypothesis, given observed data:

\[ P (H_0 \mid data)\ \ \ \text{and}\ \ \ P (H_1 \mid data) \]

From high-school probability theory, you will remember the formula for conjoint probabilities:

\[ P (A\ \text{and}\ B) = P (A \mid B)\ P (B) \]

and therefore also

\[ P (B\ \text{and}\ A) = P (B \mid A)\ P (A) \]

Since

\[ P (A\ \text{and}\ B) = P (B\ \text{and}\ A) \]

we have

\[ P (A \mid B)\ P (B) = P (B \mid A)\ P (A) \]

or

\[ P (A \mid B) = \frac {P (B \mid A)\ P (A)} {P (B)} \]

which is Bayes’ formula.

In Bayesian statistics we apply this to data and hypotheses:

\[ P (H \mid data) = \frac {P (data \mid H)\ P (H)} {P (data)} \]

where \(P (data \mid H)\) is something that we can compute (a “real” probability), \(P(H)\) is the “prior” probability that a hypothesis is true (this one is tricky, see below!), and \(P(data)\) is the probability of observing the data in the world, which is a factor that will typically vanish once we try to compute interesting things.

It is easier to work with odds than with probabilities. In the Dutch–Flemish case, we want to know how the two hypotheses (a true effect of 0 versus a true effect of 20) compare to each other, i.e. we want to the odds of H₁ versus H₀, given the data:

\[ \text{evidence in favour of} \ H_1 = \frac {P(H_1\mid data)}{P(H_0\mid data)} \]

and, equivalently, the golden grail of arguing for the null hypothesis:

\[ \text{evidence in favour of} \ H_0 = \frac {P(H_0\mid data)}{P(H_1\mid data)} \]

And we can compute these odds:

\[ \frac {P(H_1\mid data)}{P(H_0\mid data)} = \frac {P(data\mid H_1)}{P(data\mid H_0)} \frac {P(H_1)}{P(H_0)} \]

and indeed, \(P(data)\) dropped out. The first factor is simply the likelihood ratio, and the second factor is the prior odds in favour of \(H_1\), i.e. the extent to which you, as a researcher, believed in \(H_1\) versus \(H_0\) before running the experiment.

And oops, that sounds very subjective!

This subjectivity is the reason why Fisher rejected Bayesian statistics in the 1920s. Nowadays, however, Jeffreys and others have proposed more objective kinds of priors (and less stupid alternative hypotheses than \(H_1 = 20\)), and Bayesian statistics has become more popular again.

Anyway, let’s see how the Dutch–Flemish experiment would fare with Bayesian researchers. Imagine that there is a Dutch researcher who proposes that the difference between the Dutch and Flemish population means on this German-language proficiency task is 0, and that there is a Flemish researcher who proposes that the difference is 20 in favour of the Flemish population. Suppose also that these two researchers agree in advance that an impartial judge would probably consider the two hypotheses equally likely, so that

\[ \frac {P(H_1)}{P(H_0)} = 1 \]

before the experiment. The two researchers agree that they will start to believe in the other researcher’s hypothesis once the odds in favour of that hypothesis change by a factor of 100 on the basis of observed data. That is, the Dutch researcher will believe \(H_1\) as soon as

\[ \frac {P(H_1 \mid data)}{P(H_0 \mid data)} = 100 \]

and the Flemish researcher will believe \(H_0\) as soon as

\[ \frac {P(H_1 \mid data)}{P(H_0 \mid data)} = 0.01 \]

After the experiment, however, the odds have increased in favour of \(H_1\), but only by a factor 2.985 (the likelihood ratio mentioned above):

\[ \frac {P(H_1\mid exp1)}{P(H_0\mid exp1)} = \frac {P(exp1\mid H_1)}{P(exp1\mid H_0)} \frac {P(H_1)}{P(H_0)} = 2.985 \cdot 1 = 2.985 \]

So the odds are now 3 to 1 in favour of \(H_1\). Not decisive. The researchers decide to do a second experiment, which in itself gives an odds of 2 to 1 in favour of \(H_1\). As the prior odds before this second experiment are 3 to 1, the odds after the second experiment are now 6 to 1 in favour of \(H_1\):

\[ \frac {P(H_1\mid exp1,2)}{P(H_0\mid exp1,2)} = \frac {P(exp2\mid H_1)}{P(exp2\mid H_0)} \frac {P(H_1\mid exp1)}{P(H_0 \mid exp1)} = 2 \cdot 3 = 6 \]

Next, they run a third experiment, which gives an odds of 1.5 in favour of the Dutch. The odds in favour of \(H_1\) reduce to 4:

\[ \frac {P(H_1\mid exp1,2,3)}{P(H_0\mid exp1,2,3)} = \frac {P(exp3\mid H_1)}{P(exp3\mid H_0)} \frac {P(H_1\mid exp1,2)}{P(H_0 \mid exp1,2)} = 6 \cdot 1/1.5 = 4 \]

Next, the fourth experiment yields an odds of 40 in favour of the Flemish, so that the total odds become 160 in favour of \(H_1\). At this time, both researchers agree that \(H_0\) is rejected and \(H_1\) is supported. They conclude together that the Flemish population is better on this task than the Dutch population (on average).

In general, this method can lead to acceptance of \(H_0\) just as easily as to acceptance of \(H_1\), a situation not possible with Fisheran statistics.

How Bayesian statistics is really done

This example had some silly aspects, such as that \(H_1\) was a point hypothesis. In general \(H_1\) is taken as something like “everything beside \(H_0\), with some emphasis on not-so-distant hypotheses”, i.e. \(H_1\) is a collection of weighted points:

x <- seq (from = -10, to = +10, by = 0.01)
y <- 1 / pi / (1 + x^2)
plot (x, y, type = "l",
      xlab = "effect", ylab = "probability density",
      ylim = c(-0.005, 0.4))
lines (c(-10, 10), c(0, 0))
lines (c(0, 0), c(0, 0.052))
text (x = 0, y = 0.052, pos = 3, offset = 0.6,
      labels = "H0")
text (x = 1, y = 0.25, pos = 3, offset = 0.6,
      labels = "H1")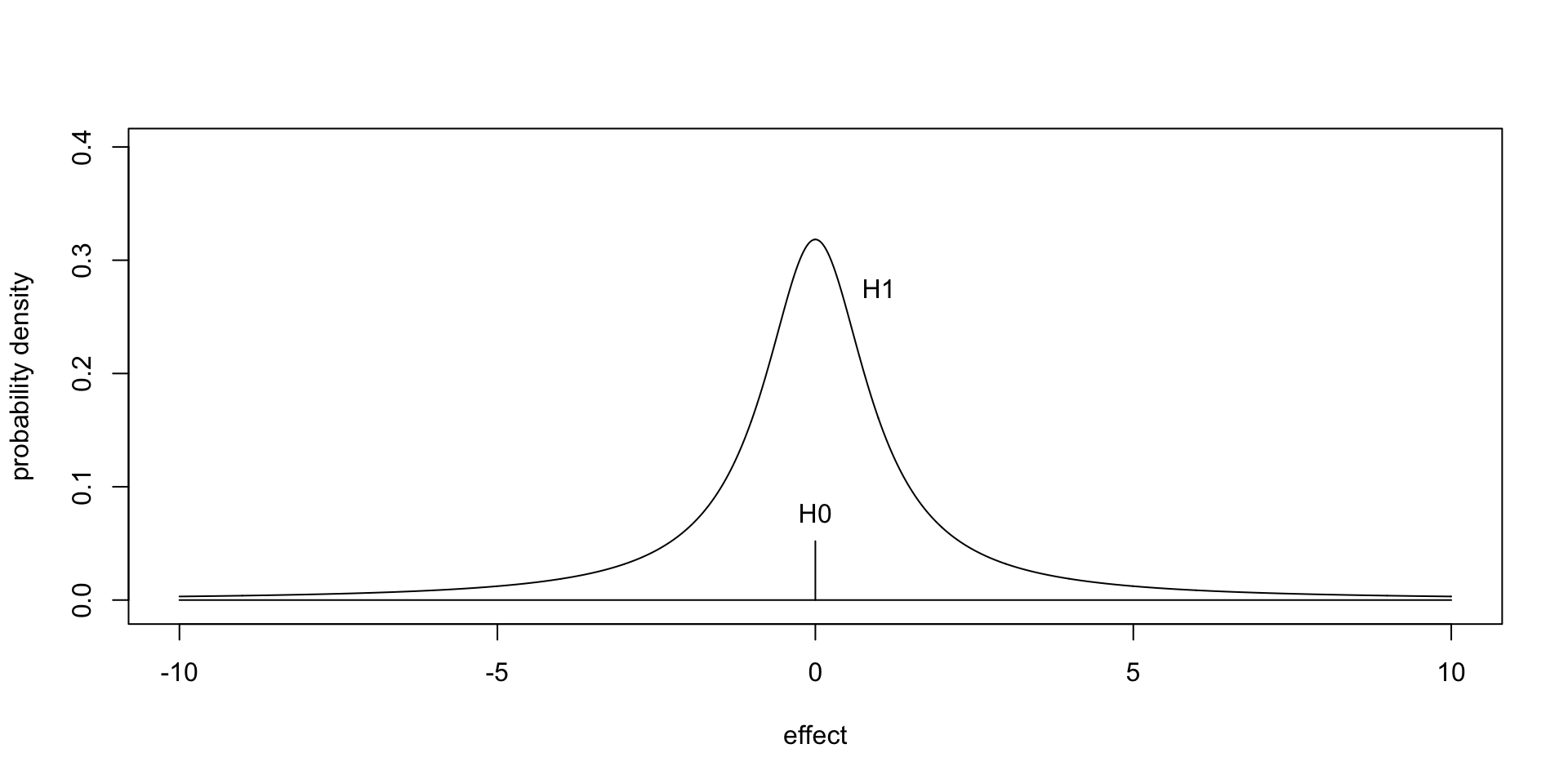

The mathematics becomes more involved, because we have to average over multiple hypotheses.

Another silly aspect was that our computations assumed that the standard deviation was known. In reality it isn’t, so we have to use “non-central t distributions” rather than Gaussian distributions, and these are mentioned in some of the papers you may have seen.