Waveforms

A sound waveform is a representation of the changes in pressure caused by the temporal evolution of a sound wave.

• Simple harmonic motion - SHM This is the type of vibratory motion produced many sources of sound, including the tuning fork. SHM is also called sinusoidal motion, and causes the sensation of a pure tone in the listener. The prerequisite for SHM is that the vibrating agent must observe Hooke's Law (F = -kx): the restoring force F must be proportional to the displacement x from equilibrium position but exerted in the opposite direction to that of the displacement. The constant of proportionality k varies according to the vibrating agent and is called the elasticity constant. The source of such a vibration moves from a position of maximum displacement, through its resting position, and then to a position of maximum displacement in the opposite direction, and back again; this is one cycle of the sinusoidal motion. This cycle repeats identically over time. Similarly, the air pressure in the sound wave caused by this motion varies from maximum condensation, through resting air pressure level, to maximum rarefaction, and back to maximum condensation. In practice, all vibrations are subject to damping, a decrease in amplitude caused by frictional forces over time.
• Dimensions of simple harmonic motion SHM may be expressed mathematically as a function of time t by the following equation:

  

  There are three attributes which determine the exact appearance of a sinusoidal waveform representing a pure tone, corresponding to the three variables other than time t in the above equation:

  • Amplitude (A) This measures the maximum change from the resting value. In our tuning fork example, one measure of amplitude is the maximum distance by which the tines are displaced from their original or resting position; another is the maximum change in pressure from normal atmospheric pressure of the resulting sound wave. The amplitude depends upon the force with which the tuning fork is struck. The amplitude of a sinusoidal waveform corresponds to the loudness of the perceived sound.
  • Frequency ( 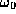) This measures the number of times per second that the waveform repeats its basic sinusoidal cycle, multiplied by 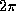. This so-called angular frequency measured in radians is used in the basic equation for SHM because it is equal to 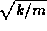, where k is the elasticity constant mentioned above and m is the vibrating mass. Frequency can also be expressed in cycles per second (cps): 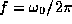, and it is this meaure of frequency which is normally used to describe spectrogram frequencies. Cycles per second are also called Hertz (Hz); for higher frequencies we use the abbreviations kHz (1000 cps), MHz (1,000,000 cps), etc. For example, the tuning fork which produces E above middle C vibrates at a frequency of 2071.13 radians per second, or 329.63 Hz. This means that in one second, the tuning fork tines move from maximum displacement in one direction to maximum displacement in the other direction and back again 329.63 times. It is this frequency which corresponds to our sensation of the pitch of E above middle C. A doubling of frequency corresponds to one musical octave; thus the E one octave higher has a frequency of 659.26 Hz. Human hearing is sensitive to frequencies from 20 Hz to 15 kHz or greater. Animals such as bats and whales can hear sounds with a frequency of up to 150 kHz. Human hearing is limited both in intensity (corresponding to amplitude) and in frequency. See Figure 3 for an diagram of the region of audibility for human beings, and for the sound level readings for some typical human auditory environments. See Figure 4 for a diagram of the frequencies associated with the 88 keys of a piano, along with the range of other orchestral instruments and human voices. We will have much more to say about the different frequencies which make up the sounds of speech; in a sense, spectrogram reading is being able to recognize those frequencies which distinguish the different phonemes.

    The notion of frequency is related to two other measures:

    • Period (T = 1/f) The period is inversely related to frequency. A frequency of 440 Hz (A above middle C, the tone by which an orchestra tunes itself) means a period of 1/440 second.
    • Wavelength ( 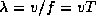) The wavelength of a given sinusoidal wave is the spatial length of one complete cycle of the wave; it is directly proportional to the wave period, and inversely proportional to its frequency. The wavelength is also dependent upon the velocity of propagation of sound v in the given medium of transmission. For example, we have seen that the speed of sound in air at 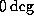is 331 m/s. The wavelength of a sinusoidal tone at 100 Hz will measure 3.31 m, whereas for a sinusoidal tone at 1000 Hz the wavelength will be 0.331 m. In water at 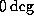, where the speed of sound is 4.3 times as great as in air at the same temperature, the wavelength for a 100 Hz tone is also greater at 14.33 m.

  • Phase ( 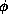) Phase measures the displacement in degrees from 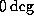at some starting reference point in time. At present it is considered that human hearing is not particularly sensitive to phase shifts, and thus in this course we shall not pay much attention to phase information.

  Figure 5 contains three sets of sine waves differing in the three defining attributes explained above:

  • Sine waves with different amplitudes may be seen in Figure 5a.
  • Sine waves with different frequencies may be seen in Figure 5b.
  • Sine waves with different phases may be seen in Figure 5c.
• Complex Waveforms Most sound waves which we encounter in our daily lives are not as simple as the sinusoidal waves which we have looked at up to this point. They may still contain more or less regular patterns of repetition (quasi-periodic waveforms), or they may be more random (aperiodic waveforms). Figure 6 contrasts an almost perfect periodic sound with two speech waveforms: Figure 6.1 shows a tuning fork, Figure 6.2 shows the quasi-periodic vowel /A/, and Figure 6.3 shows the aperiodic fricative /s/.
• Computer Waveform Files These are an encoding of sound which can be captured by a peripheral device and stored on a computer. In order to be accessible to a digital computer, the sound wave which we have been discussing must be altered in two important ways from its original form, that of a continuously varying pressure wave over some interval on the real number line:
  1. Sampling The sound wave must be sampled, that is, only a certain number of pressure readings per second are recorded. Whereas the sound wave in its original form consists of a continuously varying pressure value, telephone speech is sampled at 8000 Hz. For so-called clean speech, we need to sample at higher frequencies; in most cases this means a sampling rate of 16kHz. We will look at spectrograms with both of these sampling frequencies in this course. Compact disk recordings require still higher fidelity and as a result are sampled at 44.1kHz.
  2. Quantization In the wild, sound pressure values vary continuously in value along the real number line. In a computer waveform file, these sound pressure values must be quantized, that is, mapped to a restricted subset of possible values. Pressure values can be mapped to the range of integers between 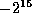and 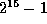, or between 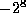and 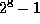, making it possible to store each sample in two bytes or one byte.

  Thus the original signal which varies continuously over time and in value is reduced to an array of 8000 or 16000 two-byte or one-byte integer values per second. The goal of this analog-to-digital conversion is to reduce the amount of data to a manageable level; even with this data reduction, each second of speech requires at least 8K bytes of storage.

• NIST Sphere waveform files In this course we will be using the NIST Sphere waveform file format, which is the standard at OGI. There are many different waveform file formats on various computer platforms, with numerous conversion programs which allow almost any waveform file to be converted to any other format.