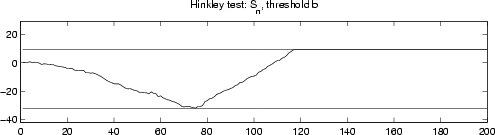
- Decide
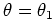
- Decide
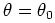
- Keep testing
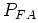 , the probability:: [
, the probability:: [
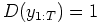 , but
, but
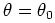 ]
]
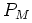 , the probability: [
, the probability: [
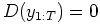 , but
, but
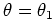 ]
]
-
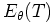 , where
, where
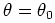 or
or 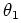
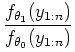 |
to positive and negative thresholds
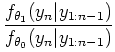 |
For an iid process, we drop the conditioning:
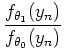 |
The drift of ![]() is defined as
is defined as
![]() . From definitions, it follows that the drifts under
. From definitions, it follows that the drifts under
![]() or
or
![]() are given by the K-L informations:
are given by the K-L informations:
- Stop, and declare
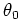 or
or
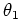 .
.
- Take one more observation.
which comes by recursively applying Bayes' rule.
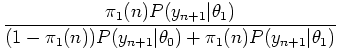 |
|||