|
A spline function f is a piecewise polynomial function defined on an interval [xmin, xmax] with specified continuity constraints, i.e., when the interval [xmin, xmax] is subdivided by points ξi such that xmin = ξ1 < ... < ξq = xmax, then within each subinterval [ξj, ξj+1) the function is a polynomial Pj of specified degree k.
A knot sequence t = {t1, ..., tn+k}, where n is the number of free parameters that specify the spline function, is derived from the ξi by placing knots at the boundary values ξi according to the order of continuity at that boundary. The most common continuity characteristics imposed on f request that for adjacent polynomials the derivatives up to order k−2 match. For example, the knot sequence of a spline of order k for a partition of [xmin, xmax] into three intervals (q = 4) will be t1 = ... = tk = xmin (= ξ1), tk+1 = ξ2, tk+2 = ξ3 , tk+3 = ... = tk+k+2 = xmax (= ξ4). This is called a simple knot sequence, because all interior knots are simple. The number of free parameters n for this case obeys a simple formula:
| n = numberOfInteriorKnots + order. |
With suitable basis functions, for example, the M-spline family Mi(x|k, t), i=1..n, we can write any spline f in the form:
| f = ∑i=1..n aiMi, |
where the Mi are defined by the following recursive formulas:
| Mi(x|1,t) = 1 / (ti+1 − ti), ti ≤ x < ti+1, 0 otherwise |
| Mi(x|k,t) = k [(x−ti)Mi(x|k−1,t) + (ti+k−x)Mi+1(x|k−1,t)] / ((k−1)(ti+k−ti)) |
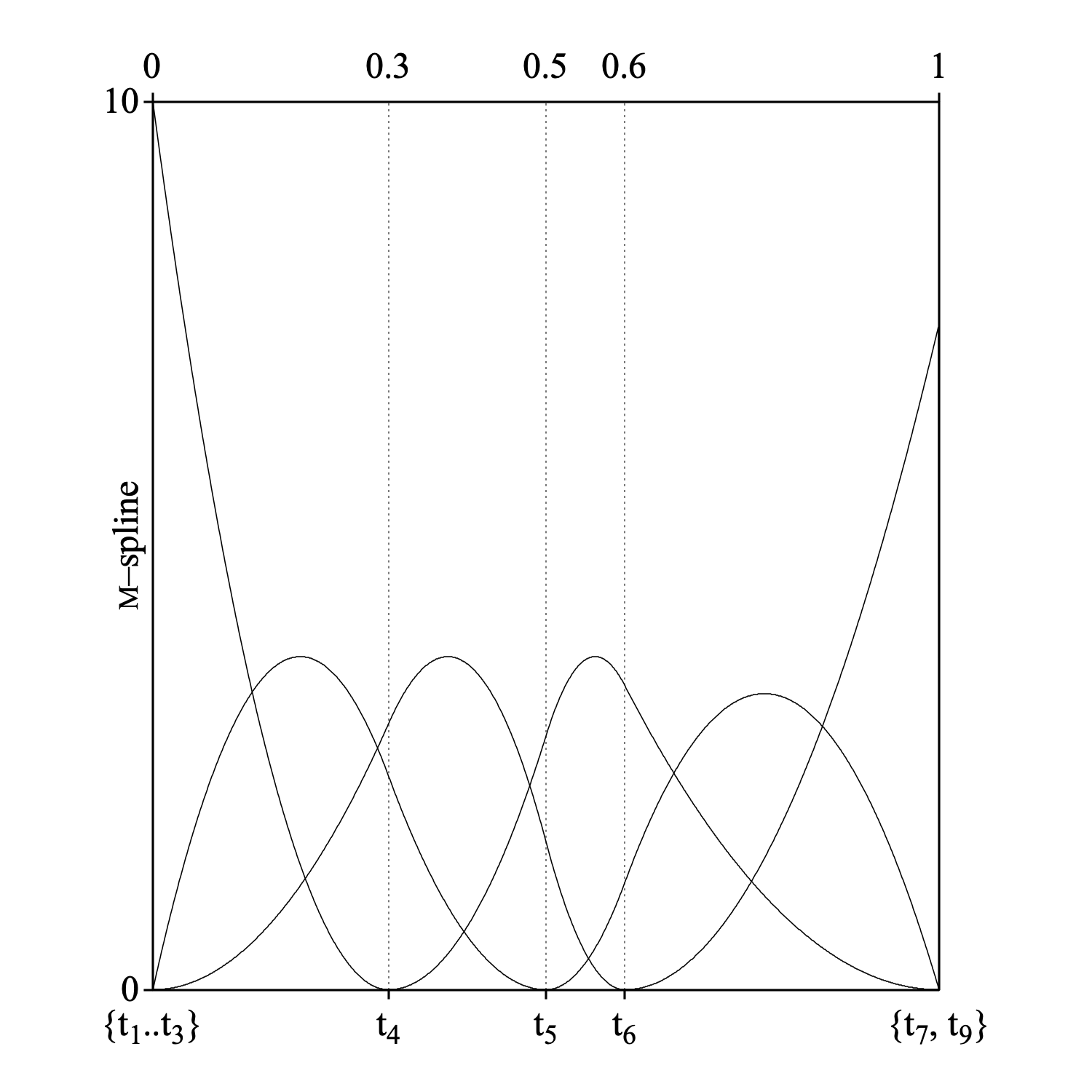
These Mi are localized because Mi(x|k,t) > 0 only when ti ≤ x < ti+k and zero otherwise. Also, we have ∫ Mi(x)dx = 1. Because of this localization a change in coefficient ai will only effect f within this interval.
The following picture shows an M-spline of order 3 on the interval [0, 1], with three interior knots at 0.3, 0.5 and 0.6.

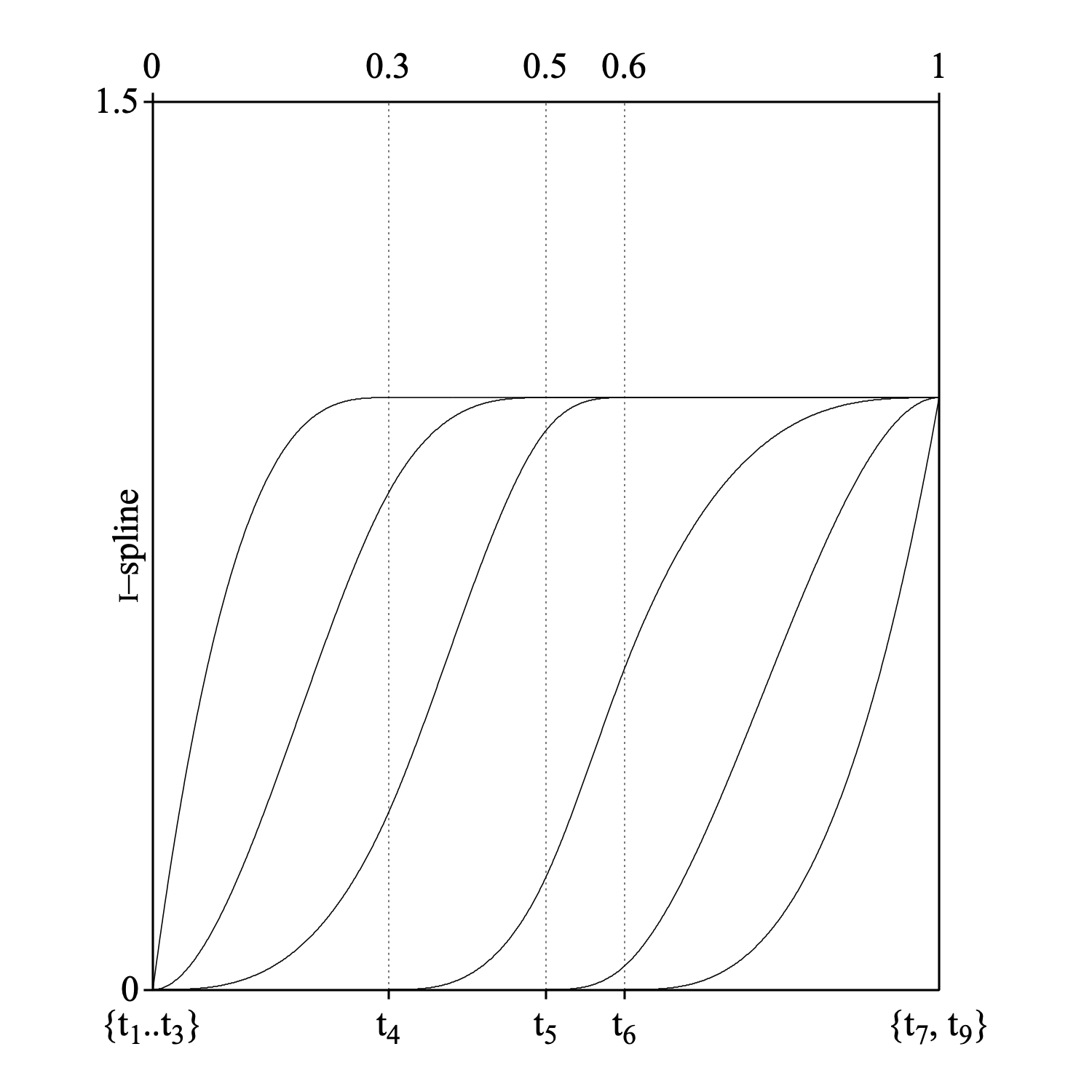
Because the M-splines are nonnegative, monotone splines can be derived from them by integration:
| Ii(x|k,t) = ∫xminx Mi(u|k,t) du |
Because each Mi(x|k, t) is a piecewise polynomial of degree k−1, each Ii will be of degree k. Now we can write:
| f = ∑i=1..n bi Ii(x|k,t) |
We can use an M-spline of order k+1 with a simple knot sequence t, for which tj ≤ x < tj+1, to put the I-spline of order k into a more convenient form:
| Ii(x|k,t) = 0, i > j |
| Ii(x|k,t) = ∑m=i+1..j (tm+k+1−tm)Mm(x|k+1,t)/(k+1), j−k ≤ i ≤ j |
| Ii(x|k,t) = 1, i < j−k |
The following figure shows the I-splines that were derived from the M-splines above.
These spline formulas were taken from Ramsay (1988) and the errors in his I-spline formulas were corrected.
© djmw 20121101