|
A command that creates a Spectrum from the selected Sound by using a fast approximation of the Discrete Fourier Transform (DFT).
In general the amount of computation necessary to calculate the spectrum of a sound that consists of N samples, is of the order of O(N log N) multiplications. If the number of samples happens to be an exact power of 2, i.e. N=2p and p integer, a special algorithm called the FFT (Fast Fourier Transform) is available to calculate the spectrum very efficiently. In normal situations, however, the number of samples seldom happens to be an exact power of 2 and the calculation of the spectrum then proceeeds much slower, especially if N happens to be a prime number a naive implementation of the DFT would calculate the spectrum in order O(N2) time. Extending the sound with zero sample values until the number of samples reaches a power of 2 enables us to use the fast FFT algorithm to calculate a fast approximation of the real spectrum. This is the traditional way to calculate the spectrum if you had chosen To Spectrum... with the fast option on.
However, there is another option to get a sound with a number of samples that equals a power of 2, namely by upsampling the sound with a suitably chosen sampling frequency. We have to calculate the new sampling frequency such that the number of samples in the upsampled sound is exactly a power of 2. Of the new upsampled sound we can use the FFT algorithm to calculate its spectrum without the need to add zero sample values. Because the upsampling results in a spectrum that contains higher frequency components than the spectrum of the original sound we have to process the just calculated spectrum by leaving out these higher frequency components to obtain the desired spectrum.
This resampled approximation generally performs better than the approximation by adding zero values.
The following script shows the three different ways to calculate a Spectrum from a given sound. We deliberately have chosen the number of samples to be prime.
sound = Create Sound from formula: "prime", 1, 0.0, 3.9799, 10000, "sin(2.0*pi*3333.0*x)"
stopwatch
spectrum_dft = To Spectrum: "no"
time_dft = stopwatch
selectObject: sound
spectrum_resampled = To Spectrum (resampled): 30
time_resampled = stopwatch
selectObject: sound
spectrum_fft = To Spectrum: "yes"
time_fft = stopwatch
On my computer from 2019 the calculation of spectrum_dft happens to be very slow because of its naive O(N2) algorithm. It takes 2.258 s while the resampled approximation only takes 0.031s and the approximation by adding zero values takes approximately 0.003 s. If the duration of the sound had been 10.0069 s, the number of samples again would be a prime number and the computing times are 14.127 s, 0.059 s and 0.005 s, respectively. This again shows that the naive implementation is very slow compared to the other two. It is also clear that resampling takes some extra time as compared to adding zero sample values.
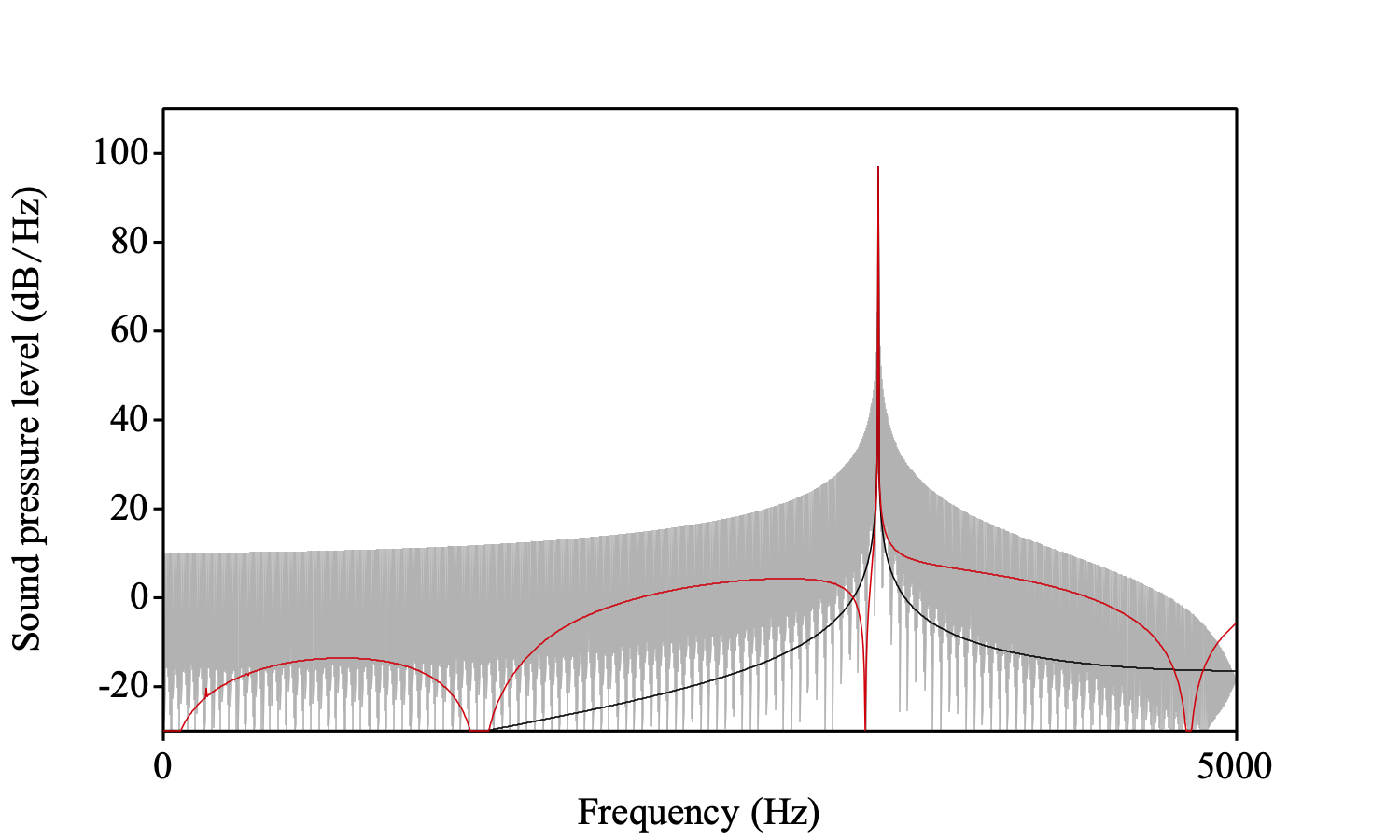
The following picture shows the spectrum_dft in black colour, the spectrum_fft in silver/grey and the spectrum_resampled in red. From the two alternative approximations of the spectrum, the resampled one looks a better approximation to the DFT than the one with zeros added.

This method was inspired by a script by Ton Wempe.
© djmw 20220105