|
OT learning 2.4. Evaluation
|
|
In an Optimality-Theoretic model of grammar, evaluation refers to the determination of the winning candidate on the basis of the constraint ranking.
In an ordinal OT model of grammar, repeated evaluations will yield the same winner again and again. We can simulate this behaviour with our NOCODA example. In the editor, you can choose Evaluate (zero noise) or use its keyboard shortcut Command-0 (= Command-zero). Repeated evaluations (keep Command-0 pressed) will always yield the following grammar:
-
| ranking value | disharmony | plasticity |
-
| NOCODA | 100.000 | 100.000 | 1.000 |
-
| PARSE | 90.000 | 90.000 | 1.000 |
In a stochastic OT model of grammar, repeated evaluations will yield different disharmonies each time. To see this, choose Evaluate (noise 2.0) or use its keyboard shortcut Command-2. Repeated evaluations will yield grammars like the following:
-
| ranking value | disharmony | plasticity |
-
| NOCODA | 100.000 | 100.427 | 1.000 |
-
| PARSE | 90.000 | 87.502 | 1.000 |
and
-
| ranking value | disharmony | plasticity |
-
| NOCODA | 100.000 | 101.041 | 1.000 |
-
| PARSE | 90.000 | 90.930 | 1.000 |
and
-
| ranking value | disharmony | plasticity |
-
| NOCODA | 100.000 | 96.398 | 1.000 |
-
| PARSE | 90.000 | 89.482 | 1.000 |
The disharmonies vary around the ranking values, according to a Gaussian distribution with a standard deviation of 2.0. The winner will still be [pa] in almost all cases, because the probability of bridging the gap between the two ranking values is very low, namely 0.02 per cent according to Boersma (1998), page 332.
With a noise much higher than 2.0, the chances of PARSE outranking NOCODA will rise. To see this, choose Evaluate... and supply 5.0 for the noise. Typical outcomes are:
-
| ranking value | disharmony | plasticity |
-
| NOCODA | 100.000 | 92.634 | 1.000 |
-
| PARSE | 90.000 | 86.931 | 1.000 |
and
-
| ranking value | disharmony | plasticity |
-
| NOCODA | 100.000 | 101.162 | 1.000 |
-
| PARSE | 90.000 | 85.311 | 1.000 |
and
-
| ranking value | disharmony | plasticity |
-
| PARSE | 90.000 | 99.778 | 1.000 |
-
| NOCODA | 100.000 | 98.711 | 1.000 |
In the last case, the order of the constraints has been reversed. You will see that [pat] has become the winning candidate:
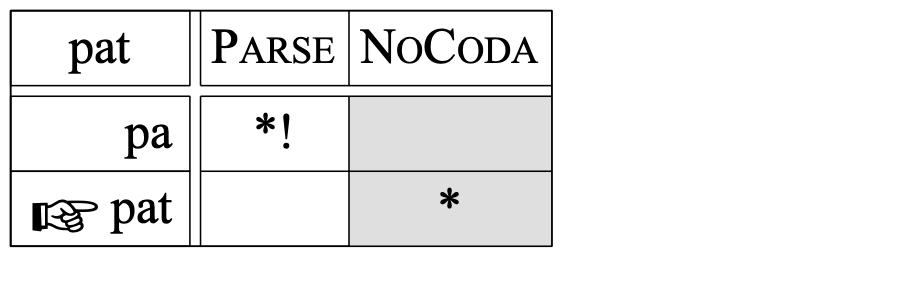
However, in the remaining part of this tutorial, we will stick with a noise with a standard deviation of 2.0. This specific number ensures that we can model fairly rigid rankings by giving the constraints a ranking difference of 10, a nice round number. Also, the learning algorithm will separate many constraints in such a way that the differences between their ranking values are in the vicinity of 10.
Links to this page
© ppgb 20070725

