|
A command to enhance the fast spectral changes, like F2 movements, in each selected Sound object.
This algorithm was inspired by Nagarajan, Wang, Merzenich, Schreiner, Johnston, Jenkins, Miller & Tallal (1998), but not identical to it. Now follows the description.
Suppose the settings have their standard values. The resulting sound will composed of the unfiltered part of the original sound, plus all manipulated bands.
First, the resulting sound becomes the original sound, stop-band filtered between 300 and 8000 Hz: after a forward Fourier transform, all values in the Spectrum at frequencies between 0 and 200 Hz and between 8100 Hz and the Nyquist frequency of the sound are retained unchanged. The spectral values at frequencies between 400 and 7900 Hz are set to zero. Between 200 and 400 Hz and between 7900 and 8100 Hz, the values are multiplied by a raised sine, so as to give a smooth transition without ringing in the time domain (the raised sine also allows us to view the spectrum as a sum of spectral bands). Finally, a backward Fourier transform gives us the filtered sound.
The remaining part of the spectrum is divided into critical bands, i.e. frequency bands one Bark wide. For instance, the first critical band run from 300 to 406 Hz, the second from 406 to 520 Hz, and so on. Each critical band is converted to a pass-band filtered sound by means of the backward Fourier transform.
Each filtered sound will be manipulated, and the resulting manipulated sounds are added to the stop-band filtered sound we created earlier. If the manipulation is the identity transformation, the resulting sound will be equal to the original sound. But, of course, the manipulation does something different. Here are the steps.
First, we compute the local intensity of the filtered sound x (t):
| intensity (t) = 10 log10 (x2 (t) + 10-6) |
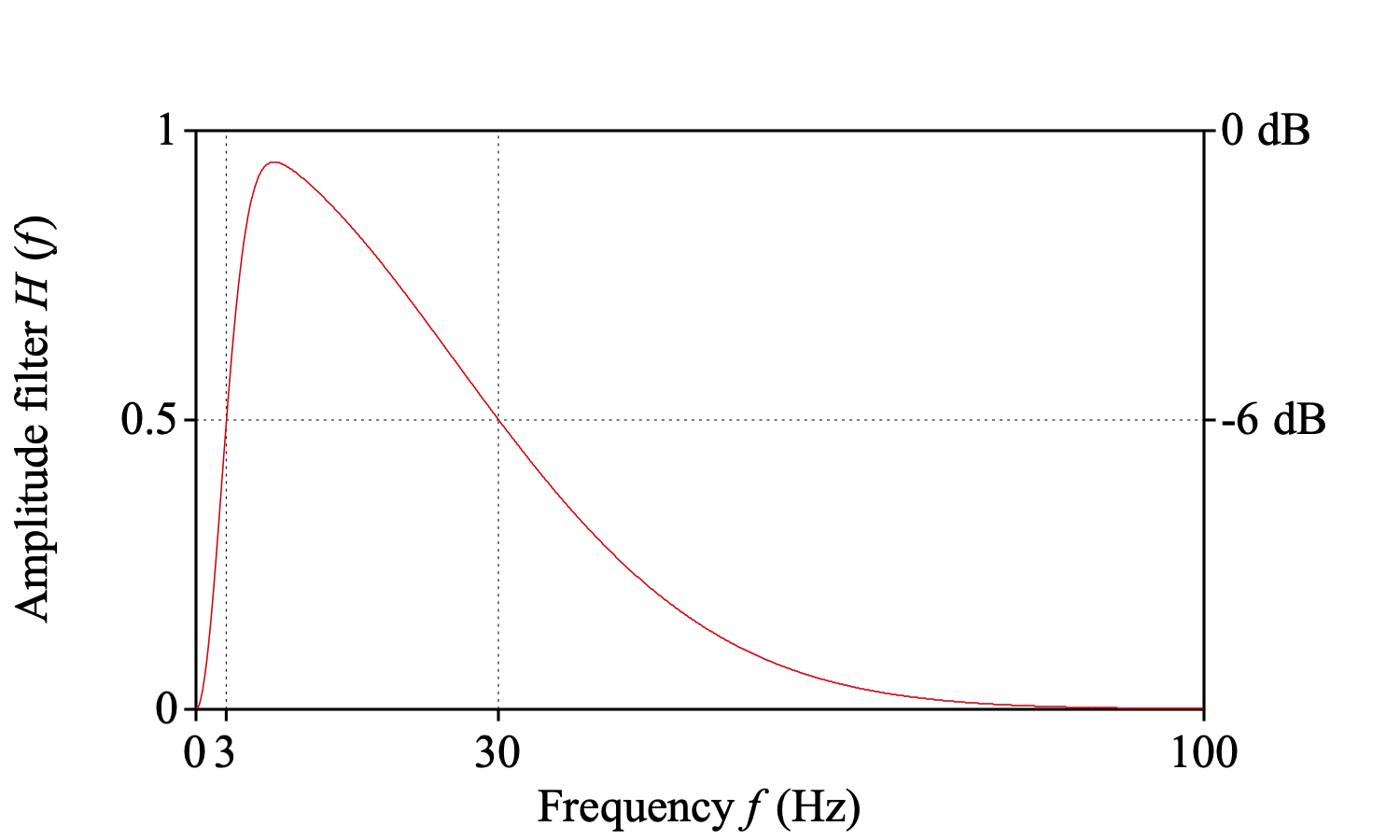
This intensity is subjected to a forward Fourier transform. In the frequency domain, we administer a band filter. We want to enhance the intensity modulation in the range between 3 and 30 Hz. We can achieve this by comparing the very smooth intensity contour, low-pass filtered at fslow = 3 Hz, with the intensity contour that has enough temporal resolution to see the place-discriminating F2 movements, which is low-pass filtered at ffast = 30 Hz. In the frequency domain, the filter is
| H (f) = exp (- (αf / ffast)2) - exp (- (αf / fslow)2) |
where α equals √ln 2 ≈ 1 / 1.2011224, so that H (f) has its -6 dB points at fslow and ffast:

Now, why do we use such a flat filter? Because a steep filter would show ringing effects in the time domain, dividing the sound into 30-ms chunks. If our filter is a sum of exponentials in the frequency domain, it will also be a sum of exponentials in the time domain. The backward Fourier transform of the frequency response H (f) is the impulse response h (t). It is given by
| h (t) = 2π√π ffast/α exp (-(πtffast/α)2) - 2π√π fslow/α exp (-(πtfslow/α)2) |
This impulse response behaves well:
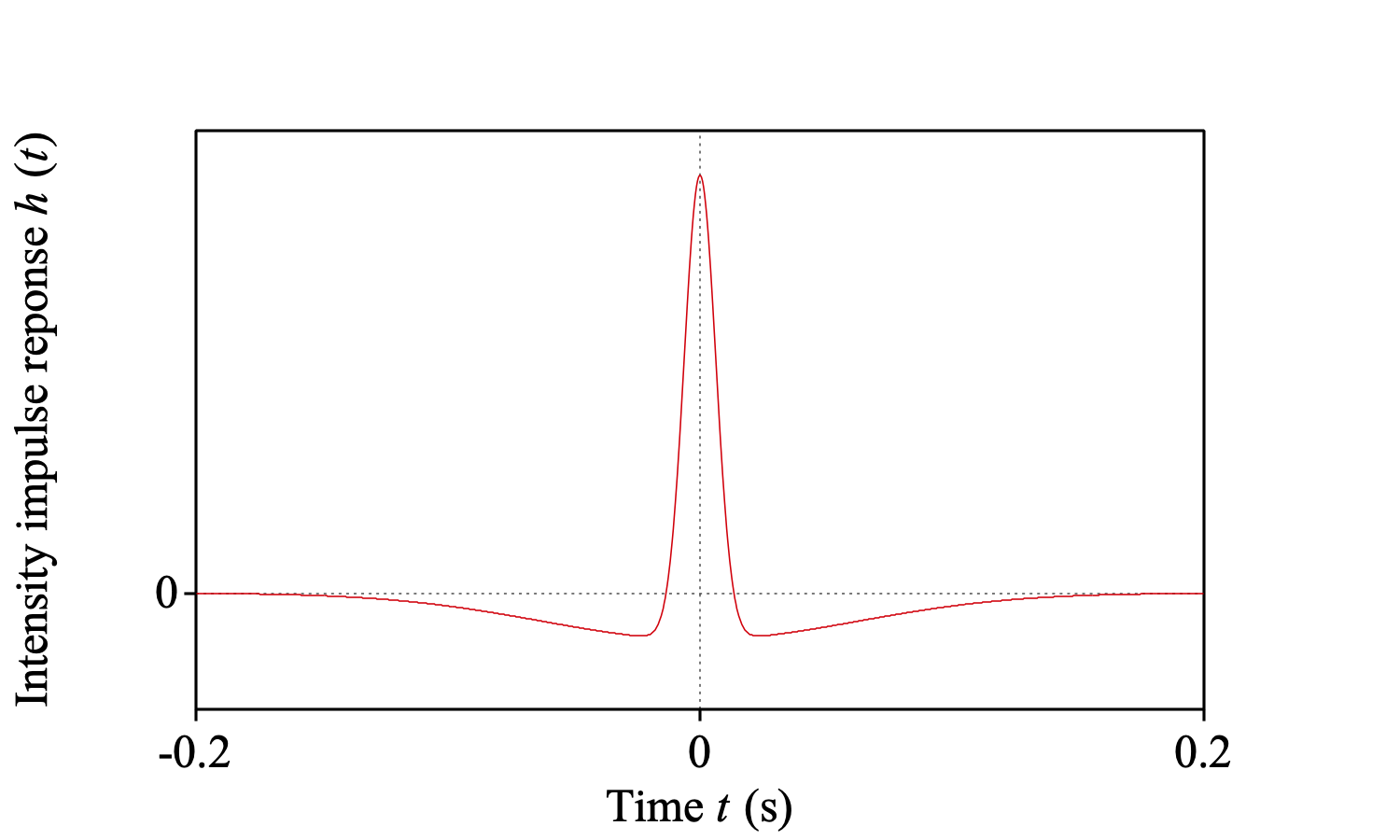
We see that any short intensity peak will be enhanced, and that this enhancement will suppress the intensity around 30 milliseconds from the peak. Non-Gaussian frequency-domain filters would have given several maxima and minima in the impulse response, clearly an undesirable phenomenon.
After the filtered band is subjected to a backward Fourier transform, we convert it into power again:
| power (t) = 10filtered / 2 |
The relative enhancement has a maximum that is smoothly related to the basilar place:
| ceiling = 1 + (10enhancement / 20 - 1) · (1/2 - 1/2 cos (π fmidbark / 13)) |
where fmidbark is the mid frequency of the band. Clipping is implemented as
| factor (t) = 1 / (1 / power (t) + 1 / ceiling) |
Finally, the original filtered sound x (t), multiplied by this factor, is added to the output.
© ppgb 20101026