A command that creates a canonical correlation object from the selected SSCP object.

Setting

Dimension of dependent variate (ny)

defines a partition of the square n x n SSCP matrix S into the parts S_yy of dimension ny x ny, S_xx of dimension nx x nx, and the parts S_xy and S_yx of dimensions nx x ny and ny x nx, respectively.

Algorithm

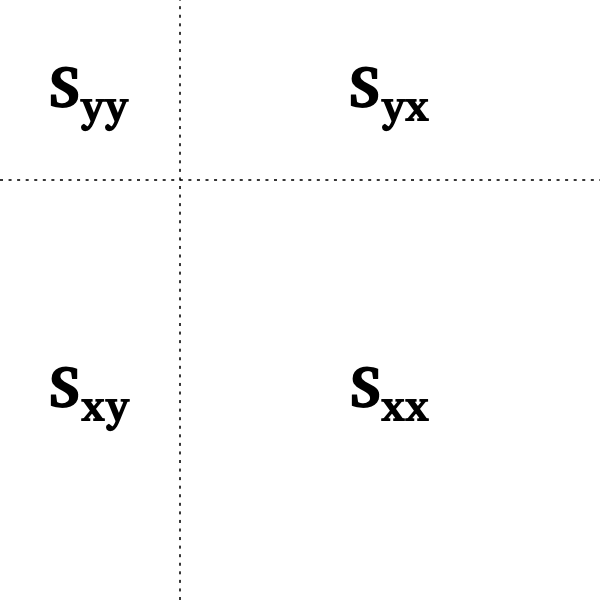
The partition for the square SSCP-matrix is as follows:

The canonical correlation equations we have to solve are:

where S_yy [ny × ny] and S_xx [nx × nx] are symmetric, positive definite matrices belonging to the dependent and the independent variables, respectively.

These two equations are not independent and we will show that both equations have the same eigenvalues and that the eigenvectors x for equation (2) can be obtained from the eigenvectors y of equation (1).

We can solve equation (1) in several ways, however, the numerically stablest algorithm is probably by performing first a Cholesky decomposition of S_xx and S_yy, followed by a generalized singular value decomposition. The algorithm goes as follows:

The Cholesky decompositions ("square roots") of S_yy and S_xx are:

where U and H are upper triangular matrices. From these decompositions, the inverse for S_xx^-1 is easily computed. Let K be the inverse of H, then we can write:

We next substitute in equation (1) and rewrite as:

This equation can be solved for eigenvalues and eigenvectors by the generalized singular value decomposition because it is of the form A′A -λ B′B.

Now, given the solution for equation (1) we can find the solution for equation (2) by first multiplying (1) from the left with S_yx′S_yy^-1, resulting in:

Now we split of the term S_xx^-1S_yx′ and obtain:

This equation is like equation (2) and it has therefore the same eigenvalues and eigenvectors. (We also proved this fact in the algorithmic section of TableOfReal: To CCA....)

The eigenvectors x is now