MDS models

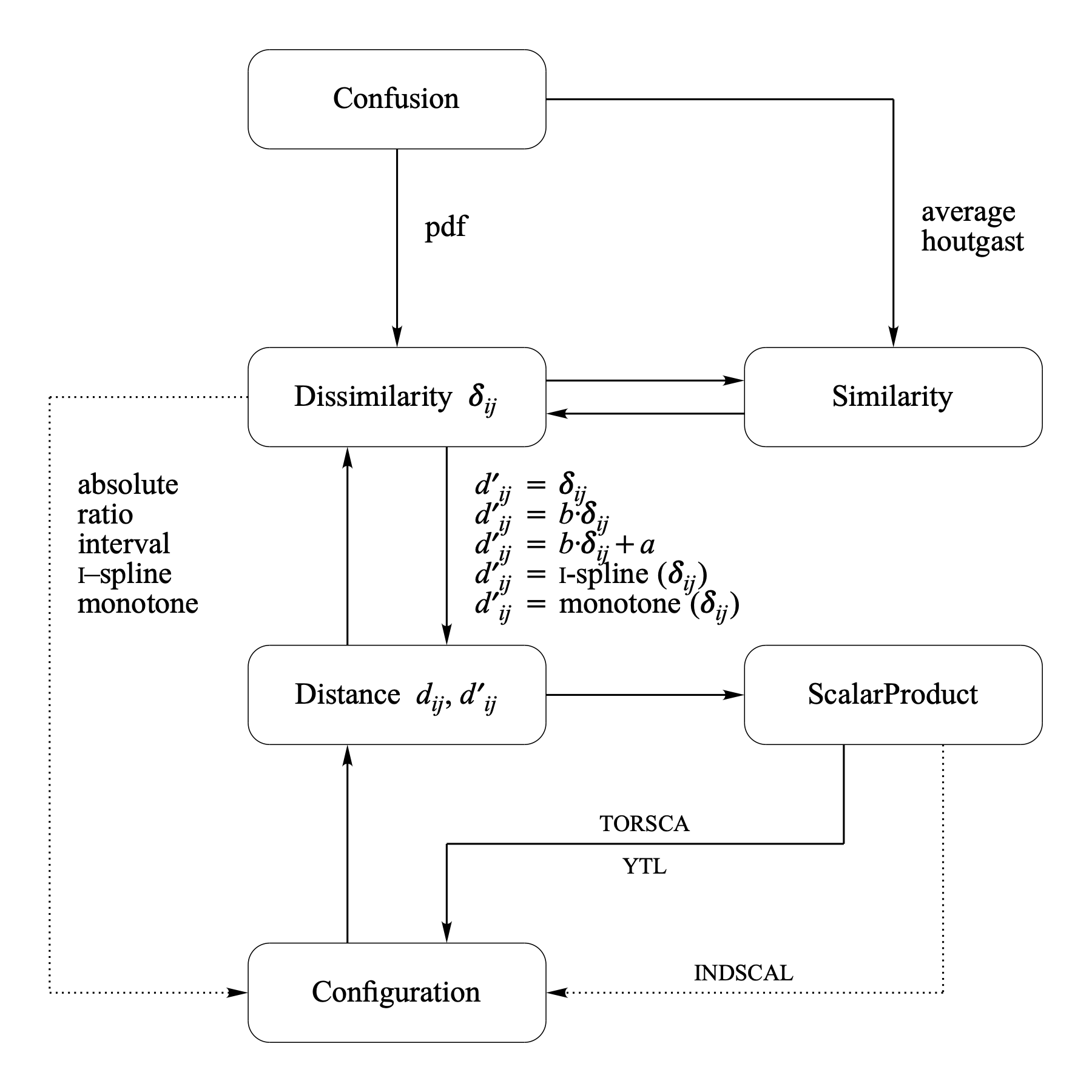
Multidimensional scaling (MDS) models are defined by specifying how given Dissimilarity data, δij, are mapped into distances of an m-dimensional MDS Configuration X. The mapping is specified by a representation function, f : δij → dij(X), which specifies how dissimilarities should be related to the distances. The MDS analysis tries to find the configuration (in a given dimensionality) whose distances satisfy f as closely as possible. This closeness is quantified by a badness-of-fit measure which is often called stress.

Representation functions

In the application of MDS we try to find a configuration X such that the following relations are satisfied as well as possible:

f(δij) ≈ dij(X)

The numbers that result from applying f on δij are sometimes called disparities d′ij. In most applications of MDS, besides the configuration X, also the function f is not completely specified, i.e., the exact parameters of f are unknown and must also be estimated during the analysis. If no particular f can be derived from a theoretical model, one often restricts f to a particular class of functions on the basis of the scale level of the dissimilarity data. If the disparities are related to the proximities by a specific parametric function we speak of metric MDS otherwise we speak of ordinal or non-metric MDS.

• absolute mds: d′ij = δij
No parameters need to be estimated.
• ratio mds: d′ij = b · δij,
where the value of b can be estimated by a linear regression of dij on δij.
• interval mds: d′ij = a + b · δij,
where the values of a and b can be estimated by a linear regression of dij on δij.
• i-spline mds: d′ij = i-spline(δij),
where i-spline(·) is a smooth monotonically increasing spline curve. The conceptual idea is that it is not possible to map all dissimilarities into disparities by one simple function.
• monotone mds: d′ij = monotone(δij),
where monotone(·) is restricted to be a monotonic function that preserves the order of the dissimilarities:
if δij < δkl, then dij(X) < dkl(X)
If δij = δkl and no particular constraint is involved for dij(X) and dkl(X) this is referred to as the primary approach to ties. The secondary approach to ties requires that if δij = δkl, then also dij(X) = dkl(X).

More information on all aspects of multidimensional scaling can be found in: Borg & Groenen (1997) and Ramsay (1988).

The most important object types used in Praat for MDS and the conversions between these types are shown in the following figure.

© djmw 20101109