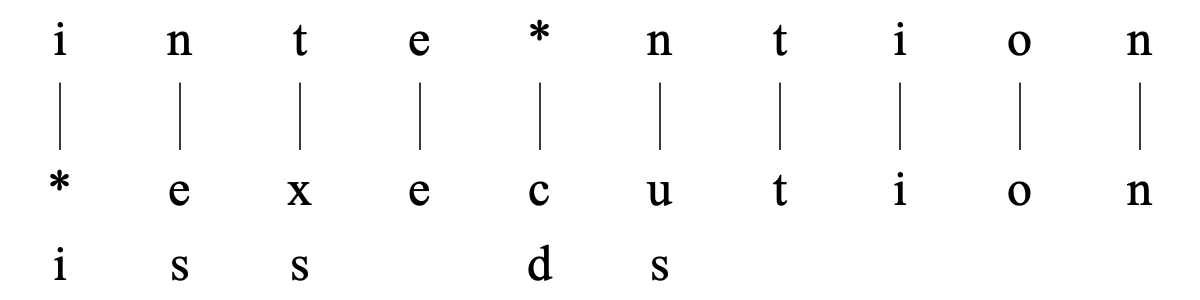
One of the types of objects in Praat.

The EditCostsTable determines the string edit costs, i.e. the costs involved in changing one string of symbols (the source) into another one (the target). String edit costs are generally divided into insertion, deletion and substitution costs. The latter terms refer to the operations that may be performed on a source string to transform it to a target string. For example, to change the source string "execution" to the target string "intention" we would need one insertion (i), one deletion (d) and three substitutions (s) as the following figure shows.

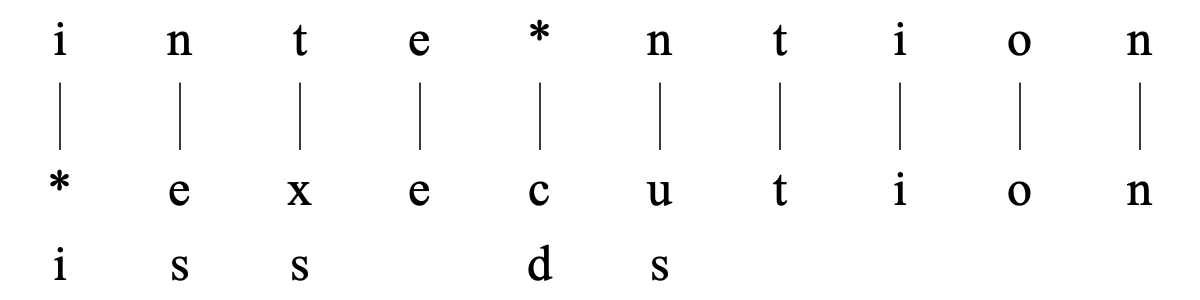
The figure above was produced with default values for the costs, i.e. the insertion and deletion costs were 1.0 while the substitution cost was 2.0. The actual edit distance between the target and source strings is calculated by the EditDistanceTable which uses an EditCostsTable to access the specific string edit costs. The figure above was produced by the following commands:

The default EditCostsTable which is in every new EditDistanceTable object has only two rows and two columns, where the cells in this EditCostsTable have the following interpretation:

Cell [1] [2]:

defines the cost for the insertion of a target symbol in the source string. The default insertion cost is 1.0.

Cell [2] [1]:

defines the cost of the deletion of a source symbol. The default value is 1.0.

Cell [1] [1]:

defines the cost of substituting a target symbol for a source symbol where the target and source symbols don't match. The default substitution cost is 2.0.

Cell [2] [2]:

defines the cost of substituting a target symbol for a source symbol where the target and source symbols do match. The deault value is 0.0.

How to create a non-default EditCostsTable

In general we can define a table for numberOfTargets target symbols and numberOfSources source symbols. These numbers do not necessarily have to be equal to the number of different symbols that may occur in the target and source strings. They only represent the number of symbols that you like to give special edit costs. The EditCostTable will provide one extra dimension to accommodate target symbol insertion costs and source symbol deletion costs and another extra dimension to represent other target and source symbols that don't have separate entries and can therefore be treated as one group. The actual dimension of the table will therefore be (numberOfTargets + 2) × (numberOfSources + 2). This is what the cells in the non-default table mean:

• The upper matrix part of dimension numberOfTargets × numberOfSources will show at cell [i] [j] the costs of substituting the i-th target symbol for the j-th source symbol.

• The first numberOfSources values in row (numberOfTargets + 1) represent the costs of substituting one of the target symbols from the target rest category for the source symbol in the corresponding column. The target rest category is the group of targets that do not belong to the numberOfTargets targets represented in the upper part of the matrix.

• The first numberOfTargets values in the column (numberOfSources + 1) represent the costs of substituting the target symbol in the corresponding row for one of the source symbols from the source rest category. The source rest category is the group of source symbols that do not belong to the numberOfSources source symbols represented in the upper part of the matrix.

• The first numberOfSources cells in the last row represent the deletion cost of the corresponding source symbols.

• The first numberOfTargets cells in the last column represent the insertion costs of the corresponding target symbols.

• Finally the four numbers in the cells at the bottom-right corner have an interpretation analogous to the four numbers in the basic EditCostTable we discussed above (but now for the rest symbols).

Example

If we extend the basic table with one extra target and one extra source symbol, then the EditCostTable will be a 3 by 3 table. The numbers in the following table have been chosen to be distinctive and therefore probably will not correspond to any practical situation.

By issuing the following series of commands this particular table can be created:

In the first line we create the (empty) table, we name it editCosts and it creates space for one target and one source symbol. The next line defines the target symbol which becomes the label of the first row of the table. Line 3 defines the source symbol which will become the label of the first column of the table. We next define the insertion and deletion costs, they fill cells [1] [3] and [3] [1], respectively. Cell [1] [1] is filled by the command in line 6. The command in line 7 fills cell [2] [1] which defines the cost of substituting any target symbol unequal to "t" for "s". The next line fills cell [1] [2] which defines the substitution costs of "t" for any source symbol unequal to "s". Finally, the command in the last line defines the little 2×2 matrix at the bottom-right that is analogous to the default cost matrix explained above. Therefore cell [2] [2] defines the cost of substituting a target symbol unequal to "t" for a source symbol unequal to "s" where the target and source symbols don't match, while cell [3] [3] defines the costs when they do match. Cell [3] [2] defines the cost of the deletion of a source symbol unequal "s", while cell [2] [3] defines the cost for the insertion of a target symbol unequal "t" in the source string.

How to use a special EditCostsTable

After creating the special EditCostsTable you select it together with the EditDistanceTable and issue the command Set new edit costs. The EditDistanceTable will then find the minimum edit distance based on the new cost values.

Links to this page

• Create empty EditCostsTable...