Wednesday 17 June: Trick: binning
This trick is not mentioned by Simmons et al. (2011). It can either raise or lower your p-values.
Binning means putting your continuous data into a finite number of cells. Let’s see what that would do to our Dutch–Flemish example, which in its correct version has a p-value of 0.02176:
dutch <- c(34, 45, 33, 54, 45, 23, 66, 35, 24, 50)
flemish <- c(67, 50, 64, 43, 47, 50, 68, 56, 60, 39)
t.test (dutch, flemish, var.equal=TRUE)##
## Two Sample t-test
##
## data: dutch and flemish
## t = -2.512, df = 18, p-value = 0.02176
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## -24.790596 -2.209404
## sample estimates:
## mean of x mean of y
## 40.9 54.4We are going to divide our data into a part 49 and a part below 49. First we sort the measurements within each group:
sort (dutch)## [1] 23 24 33 34 35 45 45 50 54 66sort (flemish)## [1] 39 43 47 50 50 56 60 64 67 68We see that for the Dutch, 7 participants had a “low” score, defined arbitrarily as any score between 0 and 49, and 3 participants had a “high” score (50 or more). For the Flemish, 3 participants had a “low” score and 7 had a “high” score. This is typical material for a \(\chi^2\)-test:
data <- rbind (c(7,3),c(3,7))
chisq.test (data)##
## Pearson's Chi-squared test with Yates' continuity correction
##
## data: data
## X-squared = 1.8, df = 1, p-value = 0.1797or
data <- rbind (c(7,3),c(3,7))
chisq.test (data, simulate.p.value = TRUE, B = 1e5)##
## Pearson's Chi-squared test with simulated p-value (based on 1e+05
## replicates)
##
## data: data
## X-squared = 3.2, df = NA, p-value = 0.1803so both the rough estimate by the \(\chi^2\)-test and the more precise computation by simulation yield a p-value around 0.18, which is not significant. By binning our data into two bins, we worsened our p-value!
So quite often, binning data is not a good idea. Instead of doing a \(\chi^2\)-test on binned count data, run a t-test on the original continuous data.
Unbin your data
Sometimes your data comes in binned. For instance, you have corpus that is divided into 18th-century, 19th-century, and 20th-century subcorpora. To track the use of construction X versus construction Y through the centuries, you count the numbers of their occurrences in all three corpora, and obtain the following frequency matrix:
centuryData <- rbind (c(14,6,6),c(3,7,13))
rownames (centuryData) <- c("X", "Y")
colnames (centuryData) <- c("18th", "19th", "20th")
centuryData## 18th 19th 20th
## X 14 6 6
## Y 3 7 13Assuming that all data points are independent, one could do a \(\chi^2\)-test to detect a difference between the relative use of constructions X and Y in the different centuries:
chisq.test (centuryData)##
## Pearson's Chi-squared test
##
## data: centuryData
## X-squared = 9.6259, df = 2, p-value = 0.008124chisq.test (centuryData, simulate.p.value = TRUE, B = 1e5)##
## Pearson's Chi-squared test with simulated p-value (based on 1e+05
## replicates)
##
## data: centuryData
## X-squared = 9.6259, df = NA, p-value = 0.00743Well, with p = 0.007 or so, this is just barely significant, regarding the fact that the reason you were looking at the diachrony of these constructions was that your eye fell on it in the corpus to begin with (data-driven “discovery”); not so interesting. But please have a look at the research question: the idea is that construction X is gradually being replaced with construction Y, and to model that we should need just one parameter (the dependence of the relative frequency of X and Y on time), rather than the two parameters (degrees of freedom) used in the \(\chi^2\)-test. More precisely, you are interested in a simple monotonic diachronic change in the X/Y ratio (an S-curve), rather than in the possibility that the X/Y ratio is low in the 18th and 20th centuries but high in the 19th century (an inverted U-curve). In other words, the columns are ordered: they provide an ordinal, or probably even interval, variable, rather than a nominal variable.
Even more important is the problem of having the data in bins while that is not necessary. The corpus labels all its data with at least the year, so the factor “time” does not have to be represented coarsely by centuries; it can be represented in a much finer-grained manner by years.
Here is the data as it comes from a simple tab-separated table file with three columns:
yearData <- read.delim ("binning_year_X_Y.txt")
yearData## year X Y
## 1 1710 1 0
## 2 1717 1 0
## 3 1722 1 0
## 4 1722 1 0
## 5 1739 1 0
## 6 1749 1 0
## 7 1751 1 0
## 8 1755 1 0
## 9 1761 1 0
## 10 1765 0 1
## 11 1777 1 0
## 12 1779 1 0
## 13 1789 0 1
## 14 1789 1 0
## 15 1791 0 1
## 16 1795 1 0
## 17 1799 1 0
## 18 1813 1 0
## 19 1815 0 1
## 20 1830 1 0
## 21 1839 1 0
## 22 1848 0 1
## 23 1849 1 0
## 24 1860 1 0
## 25 1865 0 1
## 26 1871 0 1
## 27 1876 0 1
## 28 1889 0 1
## 29 1890 1 0
## 30 1898 0 1
## 31 1901 1 0
## 32 1904 0 1
## 33 1906 1 0
## 34 1917 0 1
## 35 1921 1 0
## 36 1930 0 1
## 37 1936 1 0
## 38 1946 0 1
## 39 1946 1 0
## 40 1947 0 1
## 41 1948 1 0
## 42 1954 0 1
## 43 1959 0 1
## 44 1969 0 1
## 45 1971 0 1
## 46 1980 0 1
## 47 1991 0 1
## 48 1993 0 1
## 49 1999 0 1plot (yearData$year, jitter (yearData$Y, amount = 0.02),
xlim = c(1700, 2000), ylim = c(-0.2, 1.2),
xlab = "year", ylab = "construction",
yaxt = "n")
axis (2, at = c(0.0, 1.0), labels = c("X", "Y"), las = 1)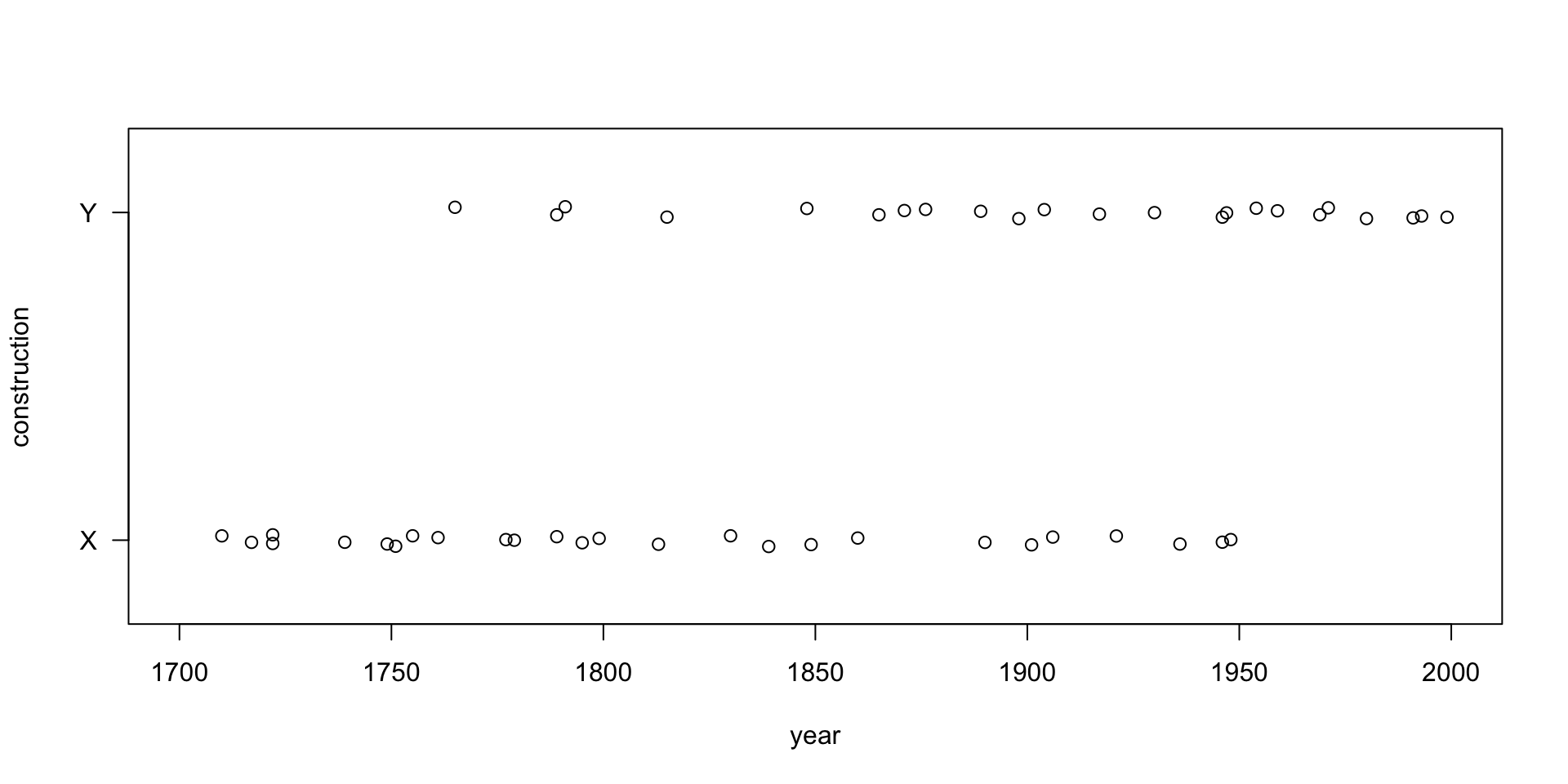
This is really the underlying data:
aggregate (yearData[,c("X","Y")], by = list(floor(yearData$year/100)), FUN = sum)## Group.1 X Y
## 1 17 14 3
## 2 18 6 7
## 3 19 6 13model <- glm (data = yearData, formula = cbind(Y, X) ~ year, family = "binomial")
summary (model)##
## Call:
## glm(formula = cbind(Y, X) ~ year, family = "binomial", data = yearData)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.7067 -0.7566 -0.4232 0.8212 1.9013
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -28.819812 8.574424 -3.361 0.000776 ***
## year 0.015406 0.004589 3.357 0.000787 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 67.745 on 48 degrees of freedom
## Residual deviance: 52.311 on 47 degrees of freedom
## AIC: 56.311
##
## Number of Fisher Scoring iterations: 4The p-value is now 0.00079, i.e. ten times better, a combination perhaps of asking a simpler research question and using the rawer continuous data.
intercept <- coefficients (model) ["(Intercept)"]
slopeByYear <- coefficients (model) ["year"]
plot (x = NA,
xlab = "year", ylab = "log odds in favour of construction Y",
xlim = c(1700, 2000), ylim = c(-5, +5))
abline (a = intercept, b = slopeByYear)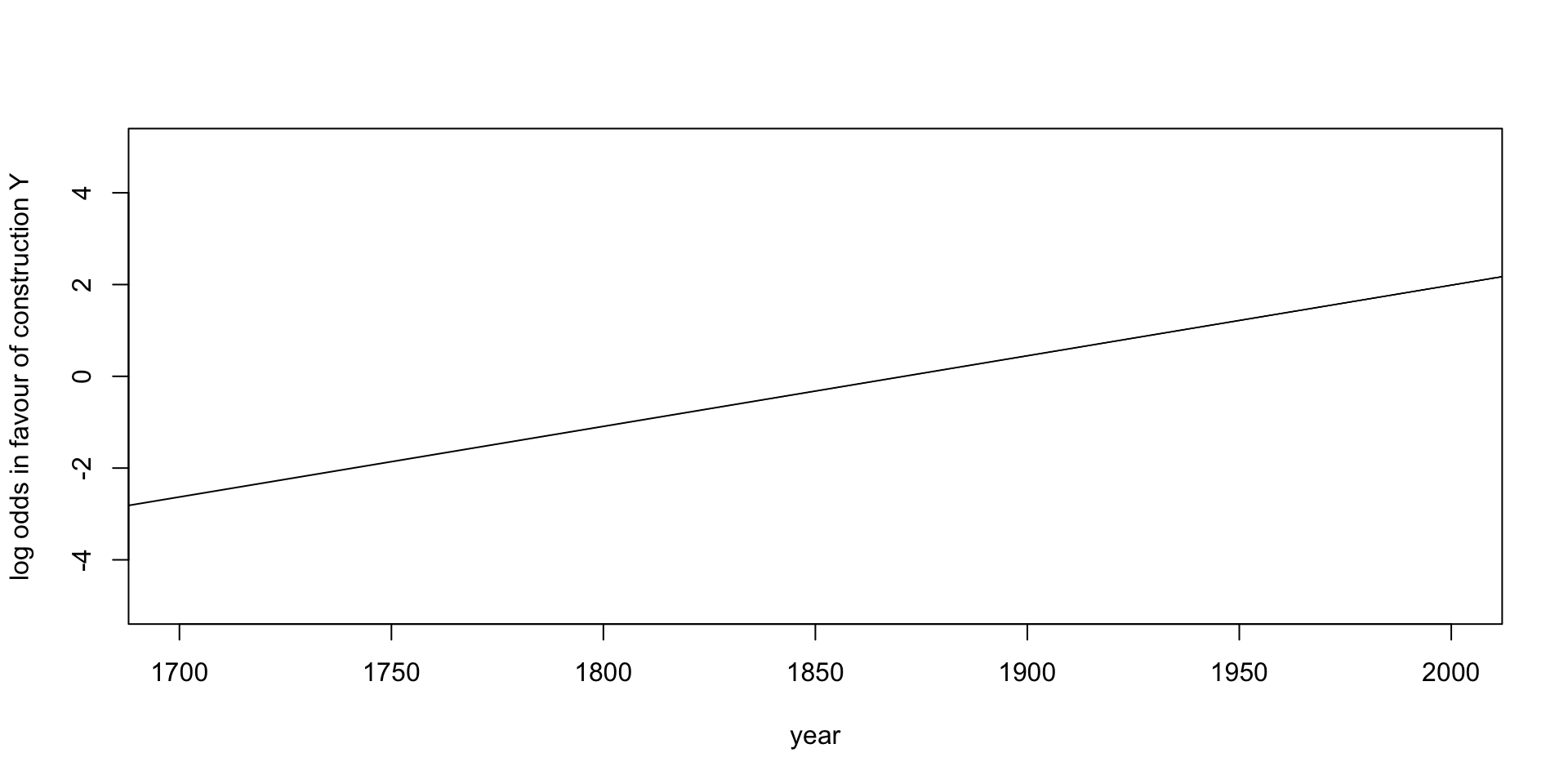
We can draw both the data and the fit in one picture:
plot (x = yearData$year, y = jitter (yearData$Y, amount = 0.02),
xlim = c(1700, 2000), ylim = c(0.0, 1.0),
xlab = "year", ylab = "probability of construction Y",
pch = 20, # the points are bullets
las = 1) # all numbers are drawn horizontally
year <- 1700 : 2000
logoddsInFavourOfY <- intercept + slopeByYear * year
oddsInFavourOfY <- exp (logoddsInFavourOfY)
probabilityOfY <- oddsInFavourOfY / (1 + oddsInFavourOfY)
lines (x = year, y = probabilityOfY)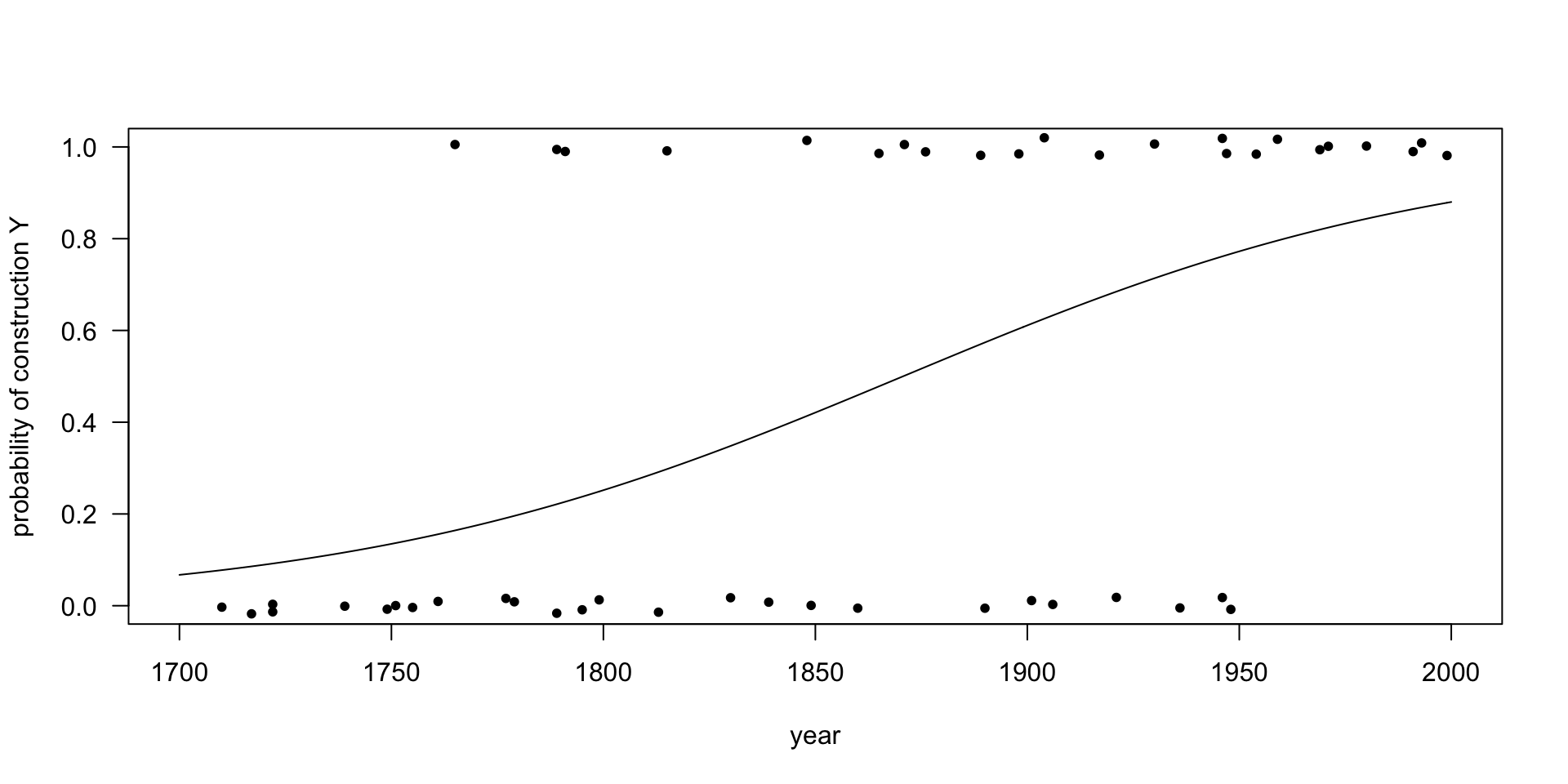
Interpretation of the intercept
That the intercept is -28.81981 means that in the year 0, the estimated log odds in favour of construction X was 28.81981. In the year 0 the estimated odds in favour of construction X was therefore exp(28.81981), which is 3.283103·1012, i.e. in the year 0 it was 3 trillion times more likely to hear construction X than construction Y.
(Of course, this is irresponsible extrapolation from data known only from the years 1700 to 2000.)
Interpretation of the year coefficient
That the coefficients of the factor “year” is 0.01541 means that every year the log odds in favour of construction Y raise by 0.01541. This means that the odds in favour of construction Y raise by a factor of exp(0.01541), which is 1.015529, i.e. the odds in favout of construction Y raise by 1.5529 percent every year.
Interpretation of the intercept and the year coefficient together
There is a turning point where we go from a situation where construction X is more likely than construction Y to a situation where construction Y is more likely than construction X. Construction X is favoured whenever the odds in favour of construction are below 1, i.e. whenever the log odds in favour of Y are below 0. The turning point comes when the log odds are exactly zero. This happens when “year” is 28.81981 / 0.01541, which is 1870. Before 1870 the language favoured construction X, and after 1870 it favoured construction Y. At least, that is our estimate from this small dataset.
Confidence intervals
We already know that the “year” coefficient has a point estimate of 0.01541 and that it is reliably greater than zero (p = 0.00079). It must have a confidence interval as well, and we already know that this confidence interval will lie symmetrically around 0.01541 and that it will be entirely positive, i.e., zero (the null hypothesis used in determining the p-value) doesn’t lie within it.
We can get the confidence interval from the model:
confint (model)## Waiting for profiling to be done...## 2.5 % 97.5 %
## (Intercept) -47.674464497 -13.50118916
## year 0.007197737 0.02548345And indeed, the confidence interval runs from 0.007198 to 0.02548, and zero doesn’t lie within. These values mean that the value by which the true log odds in favour of construction Y raise per year will lie between 0.007198 to 0.02548 (with 95 percent “confidence”), so that the factor by which the true odds in favour of construction Y raise per year will lie between exp(0.007198) = 1.007224 and exp(0.02548) = 1.025807, i.e. the odds in favour of construction Y raise by 0.7 to 2.6 percent per year.