where D are the 'counts' obtained from one previous ML iteration
(the same as in the usual ML), and 's are two La grange multipliers. It turned
out that this set of n+2 equations cannot be solved analytically as in
the usual case. Newton-Raphson procedures [3] were used to solve this set of
non-linear equations together with well chosen initial points for search. For
some phones, the data and
 need to be modified. The fitting situation is shown for two example phones in
Table 1. Durational statistics are collected from the whole TIMIT data (for
further details about this constrained training see [7]). The TIMIT training
set was used to train the 50 monophone HMMs with 3 Gaussians per state, a
diagonal covariance matrix, and n chosen as above. Table 2 shows
word-correct score improvements in both recognition and segmentation.
need to be modified. The fitting situation is shown for two example phones in
Table 1. Durational statistics are collected from the whole TIMIT data (for
further details about this constrained training see [7]). The TIMIT training
set was used to train the 50 monophone HMMs with 3 Gaussians per state, a
diagonal covariance matrix, and n chosen as above. Table 2 shows
word-correct score improvements in both recognition and segmentation.
pho original modifi modelled modelled
ne data ed + c
n
y 8.3 4.4 3.4 4 14. 6.4 8.3 3.4
4 0 9 94 8 4 9
z 10. 3.9 5 12. 4.5 10. 3.9
51 1 59 6 51 1
Table 1: Original data and , for the phones /y/ and /z/ For semi-vowel /y/
and are modified, this is also shown. n is the chosen model length. The two
right-most columns show and modelled by the usual HMM and by HMM trained with
durational constraints (+ c). Units for and are in 8 ms steps (frame shift of
the recogniser).
no constraint with duration
constraint
recognitio 80.61% 86.83% (84.41%)
n (77.73%)
segmentati 83.48% 84.48%
on
Table 2: Word correct and accuracy (in brackets) scores and segmentation
accuracy with a 20 ms margin on both directions.
Based on the statistical analysis on duration distribution using 11
contextual factors [6], 4 factors were actually chosen for context-dependent
modelling for recognition, as shown in Table 3. For each of the 1323 cells in
the factorial design, the duration and were calculated from the TIMIT
training sx and si utterances. Then parametrical models were
made for each cell using the binomial-like dpdf's (see section 2), because of
their well suited shapes for phone duration. In calculating these dpdf's,
Markov models were used (different from the phone HMMs) [7]. All cells with one
or more observations were fitted. The dpdf's for empty cells (unseen data) were
left all-zero, indicating the impossibility of those combinations of factor
levels in the training data.
factor: levels
R speaking rate 0: fast 1: average
2: slow
S stress (of 0:not 1:primary 2:
vowels) second.
L syllable if S=0,1: 0:rest;
w location in word 1:final; 2:penul.
3:mono if S=2:
0:rest; 1:final;
2:penul.
L syl. location in if Lw=0: 0:rest if
u utterance Lw=1:
0:rest;1:final;
2:penul. if Lw=2:
0:rest;
2:penul. if Lw=3:
0:rest;1:final;
2:penul.
Table 3: Contextual factors and their levels (penul=penultimate).
The durational knowledge, stored in the 1323 context-dependent (CD)
duration models, was integrated in the recogniser in a re-scoring process based
on the N-best transcriptions. An N-best program providing
transcriptions at both the word and the phone level was not available to us.
So, in order to re-score the transcriptions at the word level, using our CD
duration models at the phone level, a two-phase procedure was developed (Fig
3). In the first phase the N-best word transcriptions were generated and
in the second phase the phone-level transcriptions were generated based on the
lexical form of each word and an optional word-juncture model.
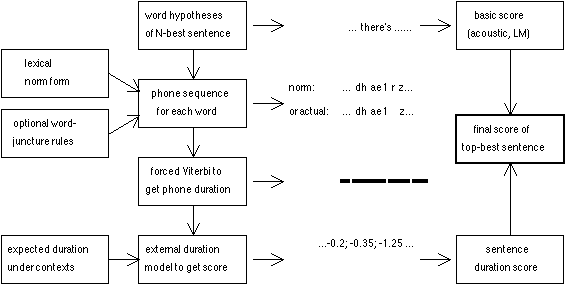 Figure 3: Procedures of re-scoring N-best transcriptions using CD duration
models. Illustrated in the middle (from top to bottom) are, a transcribed word,
the norm and an 'actual' phone transcription derived from the word-juncture
model, the estimated phone duration, and the duration scores of the phones.
Figure 3: Procedures of re-scoring N-best transcriptions using CD duration
models. Illustrated in the middle (from top to bottom) are, a transcribed word,
the norm and an 'actual' phone transcription derived from the word-juncture
model, the estimated phone duration, and the duration scores of the phones.
Modifications from norm phone to actual phone realisation were only
performed at the word junctures. This is based on the observation that most
non-norm phone transcriptions occur at word borders [6]. The word juncture
model was derived from the sx and si training utterances, and
is given as a list of rules. The input of each rule is a sequence of phones in
the juncture region of two adjacent words, as given in the lexicon for
the two words. The output is the actual phone sequence according to the
most-frequent realisation in the training set. The juncture region here
includes, either all consonents, or a single vowel, of both words. Below is an
example, where "." indicates the word border.
input output
cl k cl cl t
t.cl t
The duration scores from the CD dpdf's for phones have to be combined into
an utterance-level duration score. Direct summation (in logarithm) would
emphasise the effect of the difference in number of phones in each utterance
transcription from the N-best output. We used two procedures to
normalise for this effect. The first normalisation is at the phone level and
uses four typical values of duration defined on a phone dpdf
 (Fig. 4). These are the duration for maximum point
(Fig. 4). These are the duration for maximum point
 of
of
 for phone i, the CD duration mean
for phone i, the CD duration mean
 ,
the duration normalised
,
the duration normalised
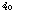 over the utterance transcription, and the actual duration
over the utterance transcription, and the actual duration
 .
Two differences are used for relative duration shifts:
.
Two differences are used for relative duration shifts:
 The second normalisation occurs at the utterance level taking into account
the total number of phones I. The duration score for an utterance is the
(weighted) sum of the two difference terms:
The second normalisation occurs at the utterance level taking into account
the total number of phones I. The duration score for an utterance is the
(weighted) sum of the two difference terms:
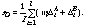 The total score for an utterance is the weighted sum (with another
weighting factor
The total score for an utterance is the weighted sum (with another
weighting factor
 )
of
)
of
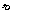 and the score of the utterance obtained in the N-best recognition
process.
and the score of the utterance obtained in the N-best recognition
process.
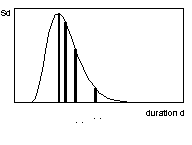 Figure 4: Four typical duration values for a dpdf.
Figure 4: Four typical duration values for a dpdf.
The baseline system for this test had 50 monophone HMMs, each with the
number of states n determined as in section 3 (ranging from 3 to 10).
However the observation pdf's of these states were further tied to 3 for each
phone. Each such pdf had 8 Gaussian components, each with a diagonal covariance
matrix. In the N-best process only 655 utterances, of the total of 1344
sx and si utterances in the TIMIT test set, had errors in the
top best transcriptions. We applied the two-phase duration modelling procedure
in this section only to this set of "wrong" utterances. Top 20 transcriptions
were generated with a word-lattice N-best algorithm and were used in the
re-scoring process. Due to the inaccuracy introduced by the separation of the
phone-level transcription from the word-level transcription, only a very tiny
increment in word correct score (3 more words correct than without re-scoring)
was obtained on this "wrong set" with a well chosen weighting factor
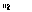 .
Experiments on the whole set of 1344 utteranes were not yet performed, but it
has to be expected that the word-correct score for the whole set will only
decrease after durational re-scoring with the current algorithm.
In this paper we tried to perform context-dependent duration modelling with
context-free HMMs. The durational behaviour of the standard (linear) HMM is
revealed to be rich (thus providing more than just a minimum duration), but the
model parameters need to be adjusted to fit the data durational statistics at
the segment level. Constrained training was performed and improvements were
obtained. Context-dependent duration information was collected based on
statistical analyses, and was then added to the system with a post-processing
process using N-best transcriptions. Actual improvement in word-correct
score was hindered by the lack of a good N-best algorithm. Future
research will involve the implementation of our context-dependent duration
models with a better N-best algorithm, and a systematic optimisation
among the various system components.
.
Experiments on the whole set of 1344 utteranes were not yet performed, but it
has to be expected that the word-correct score for the whole set will only
decrease after durational re-scoring with the current algorithm.
In this paper we tried to perform context-dependent duration modelling with
context-free HMMs. The durational behaviour of the standard (linear) HMM is
revealed to be rich (thus providing more than just a minimum duration), but the
model parameters need to be adjusted to fit the data durational statistics at
the segment level. Constrained training was performed and improvements were
obtained. Context-dependent duration information was collected based on
statistical analyses, and was then added to the system with a post-processing
process using N-best transcriptions. Actual improvement in word-correct
score was hindered by the lack of a good N-best algorithm. Future
research will involve the implementation of our context-dependent duration
models with a better N-best algorithm, and a systematic optimisation
among the various system components.
The experience in this work shows a possibility to integrate long-term speech
features into the frame-level-based HMM technique. Integrating
context-dependent information (of e.g. duration or pitch) in the last step of
post-processing provides a simple system structure, and has the advantage of
being able to correct any modelling errors that might have been made by the
statistical modelling of other system components, no matter how "perfect" these
components are designed.
- 1. Lee, K.-F. Automatic speech recognition: the development of the
Sphinx system, Kluwer Academic Publishers, Boston, 1989.
- 2. Levinson, S. E., "Continuous variable duration hidden Markov models for
automatic speech recognition", Computer Speech and Language, 1(1), 1986,
pp 29-45.
- 3. Press, W.H., Flannery, B.P., Teukolsky, S.A. & Vetterling, W.T.
Numerical recipes in Pascal, Cambridge Univ. Press, 1989.
- 4. Mitcell C., Harper, M. & Jamieson, L "On the complexity of explicit
duration HMM's", IEEE Transactions on Speech and Audio Processing, 3(3), 1995,
pp 213-217.
- 5. Papoulis, A. Probability & statistics, Prentice-Hall, Inc.,
Englewood Cliffs, NJ, 1990.
- 6. Pols, L.C.W., Wang, X. & ten Bosch, L.F.M. "Modelling of phone
duration (using the TIMIT database) and its potential benefit for ASR",
presented to Speech Comm.
- 7. Wang, X. Integrating knowledge on segmental duration in HMM-based
continuous speech recognition, Ph.D. thesis, University of Amsterdam, in
preparation.